Hồi quy logit giản đơn
Mô hình không – null model
Phần Beginning Block phân tích mô hình chỉ với hằng số trong biểu thức (đôi khi còn gọi là mô hình không – null model). Hằng số có ý nghĩa tương tự như hằng số cắt trong hồi quy OLS.

– Bảng Iteration History thể hiện lịch sử lặp của mô hình null. Ở đây quá trình lặp dừng ở bước 1 bởi vì giá trị tham số (hằng) không thay đổi nhiều hơn 0.001. Giá trị -2 Log likelihood (-2 LL) cho biết phần phương sai chưa được giải thích trong mô hình. Giá trị (-2 LL) này càng nhỏ thì mô hình càng phù hợp.

– Bảng Classification Table cho biết mức phù hợp của mô hình null trong việc nhận diện đối tượng. Các dòng thể hiện số trường hợp (đối tượng) ở mỗi nhóm trong dữ liệu thực và các cột thể hiện các trường hợp được nhận diện bởi mô hình. Giá trị phần trăm giải thích chung của mô hình (Overall Percentage) cho biết mức độ chính xác của mô hình là 50% (bằng với mức xác suất ngẫu nhiên).
3.Mô hình hoàn chỉnh
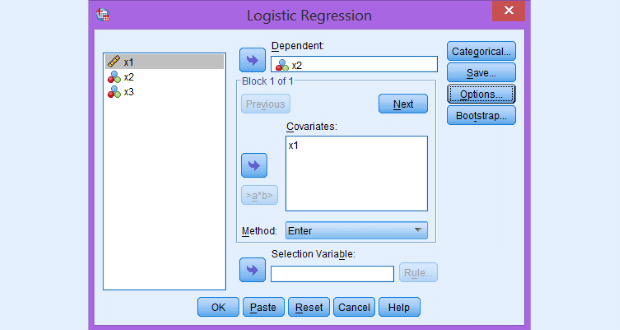
Giá trị số đi sau chữ Blocks cho biết số khối của được thiết lập ở ô Covariates của biến giải thích ở bước 2. Một khối mới được tạo bằng cách bấm nút Next và nhập các biến giải thích vào ô Covariates. Trong minh họa ví dụ này, chúng ta chỉ có một khối hay chỉ có một biến (hoặc một tập biến trong trường hợp hồi quy logit đa biến), do vậy, mô hình hoàn chỉnh chính là kết quả trong phần Block 1 bên dưới.
- Bảng Iteration history thể hiện sự thay đổi các tham số ước lượng và giá trị (-2 LL) theo các bước lặp. Kết quả cho thấy mô hình kết thúc ở bước lặp thứ 3 bởi các tham số ước lượng không thay đổi nhiều hơn 0.001. Giá trị (-2 LL) ở bước lặp này bằng 199.466 nhỏ hơn 204.944 cho thấy kết quả được cải thiện hơn so với mô hình null.

- Bảng Omnibus Tests of Model Coefficients cho biết giá trị chi bình phương ở mỗi bước của mô hình. Ở ví dụ này, chúng ta chỉ có một bước từ mô hình null đến mô hình hoàn chỉnh, vì vậy cả 3 giá trị này đều giống nhau. Mức ý nghĩa p-value bằng 0.04 cho thấy có sự khác nhau giữa mô hình hoàn chỉnh và mô hình null chỉ có mỗi hằng số ban đầu. Điều này có nghĩa biến giải thích có tác động ý nghĩa thống kê đến biến phụ thuộc.
- Bảng Model Summary thể hiện giá trị (-2 LL) cùng với các giá trị \({R^2}\) được tính toán theo Nagelkerke và Cox & Snell. Các giá trị \({R^2}\) này không có ý nghĩa đo lường mức độ phù hợp của mô hình như trường hợp \({R^2}\) của hồi quy OLS. Chúng là các \({R^2}\) giả (pseudo-\({R^2}\)). Các giá trị \({R^2}\) giả này chủ yếu dùng để so sánh các mô hình khác nhau trên cùng một tập dữ liệu hoặc cùng một biến phụ thuộc để xem mô hình nào là tốt hơn. Mô hình tốt hơn sẽ có \({R^2}\) giả cao hơn. \({R^2}\) tính toán theo Nagelkerke được tính theo cách \({R^2}\) nằm trong khoảng 0 đến 1; còn giá trị \({R^2}\) tính toán theo Cox & Snell nhằm làm mô hình tốt hơn, nhưng nó có thể nhận giá trị lớn hơn 1.
- Bảng Hosmer and Lemeshow Test thích hợp để kiểm tra mức độ phù hợp của mô hình với kiểm định chi bình phương. Tuy nhiên, giá trị kiểm định này có khuynh hướng bị phóng đại khi cở mẫu tăng. Trong ví dụ này, với giá trị chi bình phương (8 bậc tự do) bằng 8.019, p = 0.432 > 0.05, điều đó cho thấy các giá trị dự báo của mô hình không khác so với giá trị quan sát (nghĩa là mô hình giải thích các quan sát tốt).

- Bảng Contingency Table for Hosmer and Lemeshow Test tổng hợp các giá quan sát (observed) và các giá trị kì vọng (expected) cho mỗi nhóm của biến phụ thuộc được sử dụng khi tính toán chi bình phương ở bảng Hosmer and Lemeshow Test.
- Bảng Classification Table cho biết mức độ phù hợp của mô hình hoàn chỉnh trong việc giải thích các quan sát. Một mô hình hoàn hảo sẽ thể hiện số quan sát giải thích được trên đường chéo. Các dòng thể hiện số quan sát trong dữ liệu thực và các cột thể hiện số quan sát được giải thích trong mỗi nhóm của mô hình. Giá trị phần trăm giải thích chung Overall Percentage cho biết phần trăm giải thích đúng của mô hình.
Trong ví dụ, mô hình hoàn chỉnh giải thích được 66% các quan sát của dữ liệu. So với mô hình null thì mô hình hoàn chỉnh giải thích tốt hơn 16%, tuy nhiên, còn một cách khác đánh giá mức độ giải thích của mô hình. Theo quy tắc kinh nghiệm, phần trăm giải thích đúng của mô hình phải lớn hơn hoặc bằng giá trị phần trăm thay đổi + 25%. Trong đó, phần trăm thay đổi được tính bằng tổng bình phương của tỉ lệ phằm trăm các quan sát trong mỗi nhóm. Giả sử chúng ta có 250 quan sát ở nhóm 0 và 150 quan sát ở nhóm 1 của biến phụ thuộc thì phần trăm thay đổi sẽ bằng: \({\left( {{\textstyle{{250} \over {400}}}} \right)^2} + {\left( {{\textstyle{{150} \over {400}}}} \right)^2} = 0.532 = 53.2\% \). Như vậy trong ví dụ này, phần trăm thay đổi của chúng ta là 50% và theo quy tắc kinh nghiệm giá trị Overall Percentage thấp hơn 50% + 25% = 75%. Điều đó cho thấy mức độ giải thích của mô hình chưa thực sự tốt.

Bảng Variables in the Equation cho biết hệ số (B), sai số chuẩn, giá trị kiểm định Wald, bậc tự do, mức ý nghĩa cũng như giá trị tỉ số khả dĩ Exp(B) của từng biến giải thích trong hồi quy logit.
- Hệ số (B) ở đây chính là hệ số \(\beta \) trong phương trình hồi quy ứng với giá trị cao hơn (ở đây là 1 > 0). B càng gần 0 thì mức ảnh hưởng của nó càng nhỏ.
- Kiểm định Wald (cùng với mức ý nghĩa p-value) được sử dụng để đánh giá các hệ số ước lượng có khác 0 hay không. Kết quả cho thấy giá hệ số B của x1 bằng -0.045 và p-value = 0.006 cho thấy kết quả có ý nghĩa thống kê mức 1%. \(\beta \) âm cho thấy một mối liên hệ giữa xác suất x2 và x1 là mối liên hệ nghịch đảo: xác suất x2 tăng khi giá trị của x1 giảm.
- Giá trị Exp(B) chính là tỉ số khả dĩ (odd ratio) đã trình bày ở phần trên. Giá trị Exp(B) bằng 0.956 cho thấy, khi x1 tăng 1 đơn vị thì tỉ lệ khả dĩ giảm 0.044 hay 4.4%.
\(\hat p = \frac{1}{{1 + {e^{ – (\hat \alpha + \hat \beta {x_1})}}}} = \frac{1}{{1 + {e^{ – (0.678 – 0.045{x_1})}}}}\)
Để dự báo mức xác suất xảy ra của biến x2 ta cần lập bảng tính toán sự dao động của x2 theo x1 từ các hệ số \({\hat \alpha }\) và \({\hat \beta }\) theo công thức trên. Giá trị dao động của x1 thông thường là các giá trị mà chính sách (mục tiêu nghiên cứu) muốn hướng tới để xem sự thay đổi ở x2, để từ đó xác định một giá trị chính sách (x1) phù hợp. Trong ví dụ này, tôi sẽ lập giá trị dao động của x1 theo bước nhảy là sai số chuẩn. Cụ thể như sau:
| Giá trị dự báo(x1) | Mức xác suất x2(p) | % thay đổixác suất | |
| -10 | -2,970 | 0,692 | |
| -9 | -2,673 | 0,690 | -0,41% |
| -8 | -2,376 | 0,687 | -0,42% |
| -7 | -2,079 | 0,684 | -0,42% |
| -6 | -1,782 | 0,681 | -0,42% |
| -5 | -1,485 | 0,678 | -0,43% |
| -4 | -1,188 | 0,675 | -0,43% |
| -3 | -0,891 | 0,672 | -0,44% |
| -2 | -0,594 | 0,669 | -0,44% |
| -1 | -0,297 | 0,666 | -0,44% |
| 0 | 0 | 0,663 | -0,45% |
| 1 | 0,297 | 0,660 | -0,45% |
| 2 | 0,594 | 0,657 | -0,45% |
| 3 | 0,891 | 0,654 | -0,46% |
| 4 | 1,188 | 0,651 | -0,46% |
| 5 | 1,485 | 0,648 | -0,47% |
| 6 | 1,782 | 0,645 | -0,47% |
| 7 | 2,079 | 0,642 | -0,48% |
| 8 | 2,376 | 0,639 | -0,48% |
| 9 | 2,673 | 0,636 | -0,48% |
| 10 | 2,970 | 0,633 | -0,49% |
Như vậy, ở giá trị x1 = 0, nếu ta tăng x1 thêm 1 sai số chuẩn thì xác suất xảy ra x2 tăng 0.45% và mức tăng này sẽ càng lớn khi giá trị x1 tăng dần.
CHÚ THÍCH
1. Tùy theo dạng biến phụ thuộc mà ta có thể sử dụng các phương pháp hồi quy sau:
- Biến phụ thuộc là biến liên tục thì sử dụng hồi quy đa biến (multiple regression)
- Biến phụ thuộc có dạng thang đo thứ tự thì sử dụng hồi quy thứ tự (ordinal regression)
- Biến phụ thuộc có dạng thang đo định danh thì có thể sử dụng hồi quy logit đa biến bội (Multi-nomial Logistic Regression) hoặc phân tích phân tách (Discriminant Function Analysis).
- Lưu ý: khắc phục trường hợp dữ liệu của hồi quy bị phân riêng (từng phần hoặc toàn bộ)
2. Hiểu một cách đơn giản, phương pháp hợp lý cực đại ML sẽ tính toán và chọn một ước lượng sao cho xác suất xảy ra của mẫu quan sát là lớn nhất.
