Hồi quy tuyến tính đa biến – SPSS
I. GIỚI THIỆU HỒI QUY TUYẾN TÍNH ĐA BIẾN
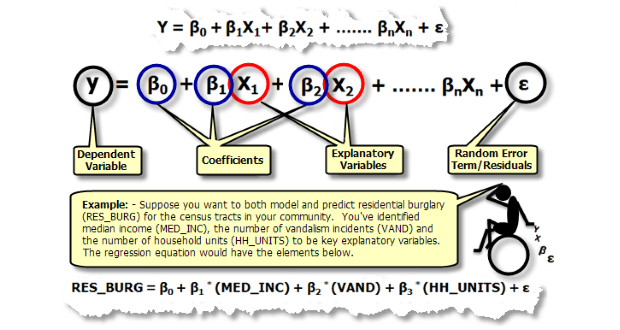
Hồi quy tuyến tính đa biến là dạng mở rộng của hồi quy tuyến tính giản đơn cho 2 hay nhiều biến độc lập. Nó được sử dụng khi chúng ta muốn dự báo một biến kết quả (biến phụ thuộc) theo giá trị của 2 hay nhiều biến giải thích (còn gọi là biến độc lập). Chẳng hạn, chúng ta muốn dự báo thu nhập của người lao động theo số năm đi học, số năm kinh nghiệm, tuổi, giới tính hoặc khu vực sinh sống của người lao động.
Xem thêm:
Các biến trong mô hình hồi quy tuyến tính đa biến phải thỏa mãn tính chất BLUE (ước lượng tuyến tính không thiên chệch tốt nhất). Tham khảo bài các khuyết tật của mô hình hồi quy để hiểu rõ hơn về ảnh hưởng của các giả định đến kết quả mô hình.
Tính chất BLUE này được thể hiện cụ thể qua các giả định quan trọng của mô hình được trình bày bên dưới.
II. CÁC GIẢ ĐỊNH CỦA HỒI QUY TUYẾN TÍNH ĐA BIẾN
Để sử dụng phương pháp hồi quy tuyến tính đa biến, dữ liệu của bạn phải thỏa mãn 7 giả định sau:
- Biến phụ thuộc trong mô hình phải là biến liên tục (có thể dạng tỉ lệ, hoặc dạng khoảng)
- Có mối quan hệ tuyến tính giữa biến phụ thuộc với các biến giải thích của mô hình. Có nhiều cách để kiểm tra mối quan hệ tuyến tính này, một trong số đó là sử dụng đồ thị phân tán giữa 2 biến. Mối quan hệ tuyến tính giữa 2 biến ở đồ thị phân tán được thể hiện như sau:

Nếu dữ liệu có dạng phi tuyến, thì chúng ta thực hiện biến đổi biến thành biến mới qua một dạng hàm phù hợp sao cho biến mới này thỏa mãn giả định tuyến tính của mô hình hồi quy.
- Dữ liệu không có chứa các điểm dị biệt (Xem thêm phát hiện điểm dị biệt).

- Có sự độc lập giữa các quan sát trong một biến. Sự độc lập giữa các quan sát có thể được kiểm tra qua kiểm định Durbin – Watson về sự tự tương quan.
- Phương sai của phần dư bằng nhau hay có sự đồng nhất về phương sai của phần dư. Sự đồng nhất về phương sai của phần dư có thể được đánh giá bằng cách sử dụng đồ thị phân tán phần dư được tạo ra sau khi biểu thức hồi quy được ước lượng.
- Không có sự đa cộng tuyến giữa các biến giải thích. Điều đó có nghĩa các biến giải thích trong mô hình không có sự tương quan cao với nhau.
- Sai số của phần dư (residuals errors) ở đường thẳng hồi quy có phân phối chuẩn hoặc xấp xỉ phân phối chuẩn. (Xem thêm Phân phối chuẩn).

