Đọc kết quả ước lượng OLS – Stata
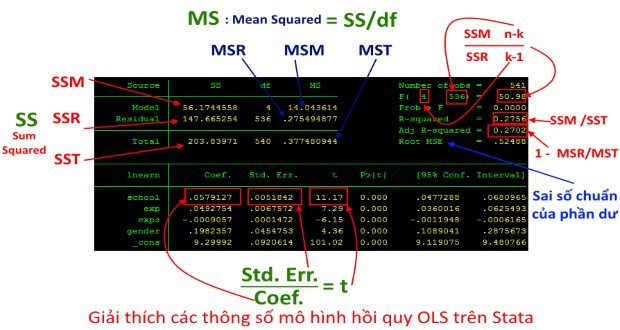
Giải thích kết quả ước lượng OLS trên phần mềm Stata
Giả sử, chúng ta muốn xây dựng mô hình dự báo thu nhập của người lao động (lnearn) theo số năm đi học (school), số năm kinh nghiệm (exp), số năm kinh nghiệm bình phương (exps) và giới tính của người lao động (female) bằng phương pháp hồi quy tuyến tính với ước lượng OLS (các biến lnearn, school, exp, exps đang ở dạng logarit). Phần minh họa sử dụng dữ liệu thực hành là ols
Trên Stata, ước lượng OLS được thực hiện bằng lệnh regress như sau:
regress lnearn school exp exps gender.
Phần kết quả (khung màu đen) và phần tính toán các thông số của ước lượng OLS được thể hiện ở hình bên dưới:

Xem thêm: Hồi quy tuyến tính trên SPSS
Với giá trị thống kê F được tính từ tổng bình phương phần dư của mô hình (SSM) và tổng bình phương phần dư chưa được giải thích (SSR) bằng 50.98 cũng cho thấy mô hình đảm bảo được độ tin cậy của mô hình (Prob>F = 0.000). Giá trị hệ số xác định \(R_{adj}^2\) bằng 0.27 cho thấy 27% sự thay đổi của các biến độc lập đã được giải thích bởi mô hình.
Kết quả của các hệ số ước lượng cho thấy tất cả các tham số ước lượng của các biến giải thích đều có ý nghĩa thống kê ở mức 1% (P>|t| = 0.000) theo giá trị của kiểm định thống kê t. Theo đó, các biến như số năm đi học, số năm kinh nghiệm có tác động dương đến thu nhập. Cứ 1 năm đi học tăng lên sẽ làm thu nhập của người lao động tăng thêm 5.96% (các yếu tố khác được giữ nguyên không đổi).
Tương tự như vậy, số năm kinh nghiệm cũng có mối tương quan dương với thu nhập của người lao động. Tuy nhiên sự tăng lên của thu nhập theo số năm kinh nghiệm có dạng hình parabol lồi, thể hiện qua hệ số của exps âm. Người lao động làm việc sau 27 năm thì thu nhập sẽ giảm dần 0.09% mỗi năm (các yếu tố khác được giữ nguyên không đổi).
Ngoài ra khi các yếu tố khác được giữ không đổi thì thu nhập của người lao động nam và nữ cũng khác nhau. Hệ số của biến giới tính bằng 0.1982357 cho biết thu nhập của lao động năm (gender = 1) cao hơn 21.9% so với thu nhập của lao động nữ (gender = 0).
Phần trình bày chỉ tập trung vào minh họa và giải thích kết quả hồi quy tuyến tính trên Stata. Các nội dung quan trọng còn lại như kiểm tra các giả định của mô hình như phân phối chuẩn của sai số, hiện tượng phương sai thay đổi, đặc tả sai mô hình, điểm dị biệt, đa cộng tuyến, tự tương quan,… các bạn tham khảo ở các link đính kèm.
GHI CHÚ VỀ HỆ SỐ CHUẨN HÓA Trong một số trường hợp, nhất là trong các thí nghiệm đo lường chúng ta giải thích sự thay đổi của biến phụ thuộc theo sự biến động từng bước nhảy sai số chuẩn của biến giải thích. Khi đó, chúng ta sử dụng các hệ số được chuẩn hóa. Để chuẩn hóa hệ số ước lượng chúng ta sử dụng công thức sau: \(b_i^* = {b_i}\frac{{{s_X}}}{{{s_Y}}}\) Trong đó: Công thức này chính là giá trị của Standardized Coefficients hay Beta trong hồi quy tuyến tính trên SPSS
Trong ví dụ trên, hệ số chuẩn hóa của biến exp bằng 0.0492754*19.12477/10.45468 = 0.0901396. Điều đó có nghĩa thay đổi 1 đơn vị độ lệch chuẩn của biến exp sẽ làm tăng 0.0901396 độ lệch chuẩn của biến lnearn.