Hồi quy tuyến tính giản đơn
I. GIỚI THIỆU HỒI QUY TUYẾN TÍNH GIẢN ĐƠN
Hồi quy tuyến tính giản đơn là bước tiếp theo của phân tích tương quan. Hồi quy tuyến tính giản đơn là một dạng đơn giản nhất của hồi quy tuyến tính[1]. Nó được sử dụng khi chúng ta muốn dự báo một biến (biến phụ thuộc/biến kết quả) theo giá trị của biến còn lại (biến độc lập/biến giải thích). Chẳng hạn, chúng ta muốn dự báo thu nhập của người lao động theo số năm kinh nghiệm.
Nếu chúng ta có từ 2 biến độc lập trở lên, khi đó, hồi quy tuyến tính giản đơn trở thành hồi quy đa biến.
II. CÁC GIẢ ĐỊNH CỦA PHƯƠNG PHÁP HỒI QUY TUYẾN TÍNH GIẢN ĐƠN
Để sử dụng phương pháp hồi quy tuyến tính, dữ liệu của bạn phải thỏa mãn một số giả định. Cụ thể các giả định đó được phát biểu như sau:
1. Hai biến trong mô hình phải là biến liên tục (có thể dạng tỉ lệ, hoặc dạng khoảng). Tham khảo bài viết các loại thang đo trong phân tích dữ liệu.
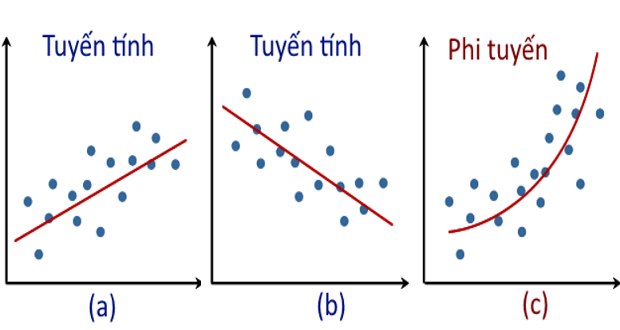
2. Có mối quan hệ tuyến tính giữa 2 biến này. Có nhiều cách để kiểm tra mối quan hệ tuyến tính này, một trong số đó là sử dụng đồ thị phân tán. Mối quan hệ tuyến tính giữa 2 biến ở đồ thị phân tán được thể hiện như sau:

Nếu dữ liệu có dạng phi tuyến, thì chúng ta thực hiện biến đổi biến thành biến mới qua một dạng hàm phù hợp sao cho biến mới này thỏa mãn giả định tuyến tính của mô hình hồi quy.
3. Dữ liệu không có chứa các điểm dị biệt (Xem thêm phát hiện điểm dị biệt).

4. Có sự độc lập giữa các quan sát trong một biến. Sự độc lập giữa các quan sát có thể được kiểm tra qua kiểm định Durbin-Watson về sự tự tương quan.
5. Phương sai của phần dữ bằng nhau hay có sự đồng nhất về phương sai của phần dư. Sự đồng nhất về phương sai của phần dư có thể được đánh giá bằng cách sử dụng đồ thị phân tán phần dư được tạo ra sau khi biểu thức hồi quy được ước lượng.
6. Sai số của phần dư (residual errors) ở đường thẳng hồi quy có phân phối chuẩn hoặc xấp xỉ phân phối chuẩn.
Tham khảo bài các khuyết tật của mô hình hồi quy để hiểu rõ hơn về ảnh hưởng của các giả định đến kết quả mô hình
III. THỰC HÀNH HỒI QUY TUYẾN TÍNH GIẢN ĐƠN TRÊN SPSS
Giả sử, chúng ta muốn biết mối quan hệ thu nhập (triệu đồng/năm) theo số năm kinh nghiệm của người lao động như thế nào? Tăng thêm 1 năm kinh nghiệm có thể cải thiện được bao nhiêu phần trăm thu nhập? Để trả lời câu hỏi này, chúng ta sử dụng phương pháp hồi quy tuyến tính giản đơn.
Sử dụng đó là bộ dữ liệu dữ liệu thực hành hồi quy. Bộ dữ liệu gồm 44 quan sát là các nhân viên làm việc ở các doanh nghiệp trên địa bàn Tp.Thủ Dầu Một. Phạm vi khảo sát trong 4 loại hình doanh nghiệp (set) gồm CTCP (A), Công ty tư nhân (B), FDI (C), và DNNN (D). Các nhân viên được được khảo sát về số năm kinh nghiệm (x), thu nhập hiện tại (y).
1.Vào Analyze \( \to \) Regression \( \to \) Linear…

– Đưa biến y vào Dependent và biến x vào ô Independent(s): như hình:

Thiết lập nút Statistics như hình

Phần này sẽ thiết lập các thông số như độ phù hợp của mô hình Model fit, hệ số ước lượngEstimates, kiểm tra hiện tượng đa cộng tuyến Collinearity diagnostics, kiểm định Durbin-Watson về sự tự tương quan. Các vấn đề này sẽ được phân tích sâu hơn trong các bài viết về chủ đề này.
3.Vẽ đồ thị phần dư của ước lượng theo giá trị dự báo để kiểm tra hiện tượng phương sai thay đổi và phân phối chuẩn của phần dư ở nút Plots như hình bên dưới:

Lưu ý: để sử dụng kiểm định Durbin-Watson thì phương trình hồi quy phải bao gồm hệ số chặn, do vậy, cần kiểm tra mục Include constant in equation ở nút Options đã được chọn.

Sau mỗi bước thiết lập ở các nút, chúng ta bấm Continue để quay về cửa sổ Univariate.
– Bấm OK để tiến hành thực hiện.