Hệ số tương quan hạng Spearman
II. MINH HỌA THỰC HÀNH TƯƠNG QUAN HẠNG SPEARMAN TRÊN SPSS
Trên SPSS, tương quan hạng Spearman được thực hiện như sau:
1.Vào Analyze \( \to \) Correlate \( \to \) Bivariate…

Cửa sổ Bivariate Correlations mở ra và đưa 2 biến none và biến discount vào ô Variables: và thiết lập nút Options… như hình bên dưới:

Lưu ý: Đảm bảo rằng Pearson và Spearman trong phần Correlation Coefficients đã được chọn.
– Bấm Continue và OK để tiến hành thực hiện.
3.Kết quả phân tích tương quan hạng Spearman
– Bảng Descriptive Statistics thống kê mô tả về giá trị trung bình, độ lệch chuẩn, và số quan sát của mỗi biến. Theo đó, số lượng sản phẩm smart phone trung bình được bán ở các cửa hàng trong trường hợp có giảm giá là cao hơn so với bán bình thường.
– Bảng Correlations cho biết kết quả tính toán hệ số tương quan Pearson và tương quan hạng Spearman được tổng hợp từ 2 bảng riêng rẻ như sau:

Kết quả cho thấy không có sự chênh lệch lớn cả về độ lớn lẫn mức ý nghĩa giải thích giữa hệ số tương quan Pearson và hệ số tương quan hạng Spearman. Cả hai đều cho thấy một mức tương quan dương tương đối (0.55 – 0.58) giữa doanh số bán hàng thông thường và doanh số bán hàng khi có giảm giá (mức ý nghĩa 1%).
Liên hệ giữa tương quan và hồi quy tuyến tính giản đơn. Phân tích tương quan có rất nhiều điểm tương đồng với hồi quy tuyến tính giản đơn, tuy nhiên, chúng ta không thể đồng nhất việc thực hiện giữa 2 phương pháp.
Tham khảo bài Tương quan và hồi quy tuyến tính giản đơn để có một cách nhìn rõ ràng hơn về 2 phương pháp này.
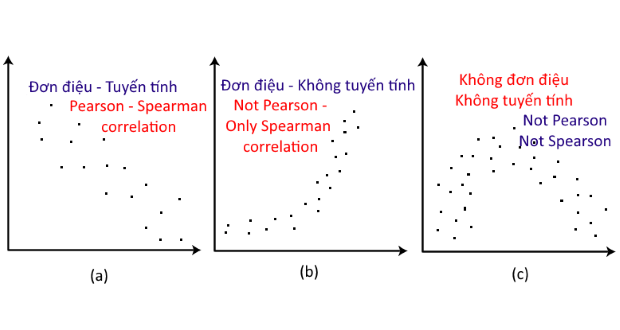
NHẬN XÉT VỀ TƯƠNG QUAN HẠNG SPERMAN VÀ TƯƠNG QUAN PEARSON
1. Nhiều người sử dụng tương quan hạng Spearman là một kiểm định thay thế tương quan Pearson khi một hoặc cả hai biến không thỏa mãn điều kiện phân phối chuẩn. Tương quan Pearson giả định rằng các dữ liệu phải có phân phối chuẩn hóa, trong khi tương quan hạng Spearman không đòi hỏi giả định này, vì vậy, mọi người nghĩ rằng tương quan hạng Spearman sẽ tốt hơn. Thực tế, rất nhiều nghiên cứu thực nghiệm cho thấy tương quan Pearson ít nhạy cảm đối với tính chuẩn hóa của dữ liệu. Điều đó có nghĩa, nếu xác suất bác bỏ H0 (mức ý nghĩa 5%) trong trường hợp dữ liệu vi phạm phân phối chuẩn thì tương quan Pearson vẫn có ý nghĩa 5%. (Edgell và Noon, 1984)[2]. Vì vậy, bạn vẫn có thể sử dụng tương quan Pearson ngay cả khi dữ liệu có chút vấn đề về phân phối chuẩn.
2. Edgell, S.E., and S.M. Noon. 1984. Effect of violation of normality on the t-test of the correlation coefficient. Psych. Bull. 95: 576-583.