Hồi quy tuyến tính – OLS – Stata

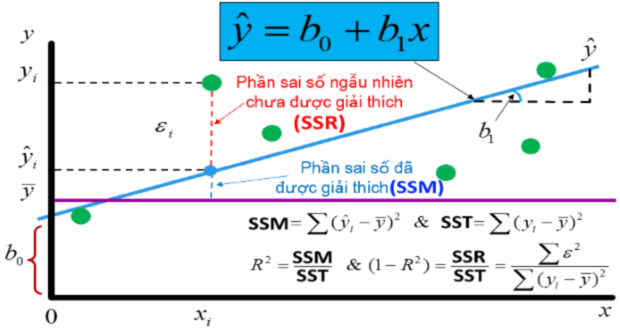
Mô hình hồi quy tuyến tính được sử dụng để xác định mối quan hệ tuyến tính giữa một (hồi quy tuyến tính giản đơn) hoặc nhiều biến giải thích (hồi quy tuyến tính đa biến) với một biến phụ thuộc dạng liên tục.

Thông thường có 3 phương pháp được sử dụng phổ biến để ước lượng mô hình hồi quy tuyến tính:

• Ước lượng bình phương thông thường nhỏ nhất (OLS)
• Ước lượng bình phương tổng quát nhỏ nhất (GLS)
• Ước lượng hợp lý cực đại (ML)

Bài viết này tập trung đi vào trình bày ước lượng mô hình hồi quy tuyến tính bằng phương pháp bình phương thông thường nhỏ nhất (OLS). Bắt đầu là phần giả định của mô hình hồi quy tuyến tính, tiếp đến là phần tính chất của ước lượng OLS, cuối cùng là phần phương pháp thực hiện.

Phần đánh giá độ tin cậy của mô hình hồi quy tuyến tính và giải thích các thông số ước lượng trên phần mềm Stata sẽ được trình bày ở bài giải thích kết quả ước lượng OLS.

Giả định mô hình hồi quy tuyến tính

• Sai số của phần dư (residuals errors) ở đường thẳng hồi quy có phân phối chuẩn hoặc xấp xỉ phân phối chuẩn.
• Phương sai sai số đồng nhất theo tất cả các quan sát.
• Sai số ngẫu nhiên sẽ độc lập thống kê lẫn nhân. Đây là giả định về không tự tương quan.
• Dữ liệu không có chứa các điểm dị biệt (Xem thêm phát hiện điểm dị biệt).
• Biến phụ thuộc trong mô hình phải là biến liên tục (có thể dạng tỉ lệ, hoặc dạng khoảng)
• Có mối quan hệ tuyến tính giữa biến phụ thuộc với các biến giải thích của mô hình. Nếu dữ liệu có dạng phi tuyến, thì chúng ta thực hiện biến đổi biến thành biến mới qua một dạng hàm phù hợp sao cho biến mới này thỏa mãn giả định tuyến tính của mô hình hồi quy.
• Không có sự đa cộng tuyến giữa các biến giải thích. Điều đó có nghĩa các biến giải thích trong mô hình không có sự tương quan cao với nhau.

Tính chất của ước lượng OLS

• Ước lượng OLS có những tính chất quan trọng sau:
• Không chệch (unbiasedness): giá trị trung bình của những tham số ước lượng sẽ bằng các tham số tổng thể hay \(E({b_i}) = {\beta _i}\)
• Phù hợp (consistency): sự khác nhau giữa tham số ước lượng và tham số tổng thể sẽ giảm khi số quan sát của mẫu dữ liệu tăng theo định lí giới hạn trung tâm.
• Hiệu quả (efficiency): phương sai của các tham số ước lượng sẽ nhỏ nhất so với các phương pháp ước lượng không chệch khác.
• BLUE (ước lượng không chệch tuyến tính tốt nhất): đây là sự kết hợp của các tính chất không chệch, tuyến tính, và hiệu quả. Theo đó, những hệ số ước lượng bi sẽ là những ước lượng không chệch tốt nhất nếu có phương sai nhỏ nhất.

Xem thêm: phát hiện và xử lý các khuyết tật của mô hình hồi quy