Tại sao phải phát hiện khuyết tật mô hình hồi quy?

Một mô hình chỉ có ý nghĩa giải thích khi các giả định của nó đã được thỏa mãn. Do vậy, trong nghiên cứu bạn cần phải kiểm tra các giả định trước khi diễn giải các kết quả của mô hình. Quá trình kiểm tra các giả định có thể được thực hiện thông qua việc “chẩn đoán” phát hiện khuyết tật có thể có của mô hình. Bài viết sau sẽ trình bày một số phương pháp (hoặc kiểm định) phổ biến và dễ dàng sử dụng để phát hiện khuyết tật này.

Ghi chú: bài viết không đi sâu vào phân tích từng loại khuyết tật, tham khảo thêm các bài viết tương ứng để hiểu rõ hơn về từng loại khuyết tật này.

1.

Đa cộng tuyến (Collinearity)

Đa cộng tuyến nghĩa là hai hay nhiều biến giải thích trong biểu thức hồi quy có mối quan hệ tuyến tính với nhau. Nếu các biến có mối quan hệ tuyến tính thì các hệ số ước lượng và thống kê T sẽ không còn hợp lý.

Đa cộng tuyến giữa các biến luôn tồn tại và khuyết tật chỉ xảy ra nếu mức độ đa cộng tuyến đủ lớn để gây ra sự thiên chệch các kết quả ước lượng.

Một số cách kiểm tra vấn đề đa cộng tuyến như sau:

• Phân tích tương quan từng cặp. Nếu giá trị tuyệt đối của hệ số tương quan giữa 2 biến lớn hơn 0.8 cho thấy có tồn tại hiện tượng đa cộng tuyến giữa 2 biến này.
• Đa cộng tuyến tồn tại trong nhiều trường hợp mô hình có \({R^2}\) lớn hơn 0.75 (một vài tài liệu đề nghị là 0.8) nhưng chỉ có vài hệ số có ý nghĩa thống kê.
• Sử dụng hệ số khuếch đại phương sai (VIF), nếu VIF của một biến lớn hơn 10 thì tồn tại hiện tượng đa cộng tuyến giữa biến đó với các biến giải thích còn lại.

2.

Tự tương quan

Tự tương quan xảy ra khi các sai số bị tương quan với nhau. Trong trường hợp này, sai số nhiễu của các quan sát khác nhau được tính từ các phân phối khác nhau không phải là phân phối của các biến giải thích. Sự tự tương quan chủ yếu xảy ra ở các dữ liệu thời gian.

Chúng ta có thể phát hiện sự tự tương quan bằng đồ thị trực quan và kiểm định Durbin – Watson.

• Vẽ đồ thị phần dư của ước lượng theo thời gian.
• Nếu đồ thị trực quan này cho thấy có vấn đề, thực hiện các kiểm định Durbin – Watson.

Kiểm định Durbin – Watson được sử dụng trong việc kiểm tra sự tự tương quan ở các dữ liệu chuỗi thời gian. Nguyên tắc của kiểm định Durbin – Watson là so sánh giá trị thống kê d với các mức tới hạn dL và dU (tra bảng ứng với mức ý nghĩa, số biến độc lập của mình và số quan sát của mẫu dữ liệu). Giá trị thống kê d được tính như sau: \(d = \frac{{\sum {{{({e_i} – {e_{i – 1}})}^2}} }}{{\sum {e_i^2} }}\)

So sánh giá trị tính toán của kiểm định với giá trị tra bảng (dL, dU)

• Nếu d < dL thì bác bỏ giả thuyết không và kết luận rằng có sự tự tương quan bậc 1. – Nếu d > dU thì chấp nhận giả thuyết không và kết luận rằng không có sự tự tương quan bậc 1.
• Nếu d nằm giữa dL và dU thì chưa thể kết luận.

Một quy tắc kinh nghiệm được sử dụng để kết luận không có sự tự tương quan bậc 1 là nếu giá trị thống kê d nằm giữa 1.5 và 2.5. d nhỏ hơn 1.5 cho biết có sự tự tương quan dương bậc 1. d lớn hơn 2.5 cho biết có sự tự tương quan âm bậc 1.

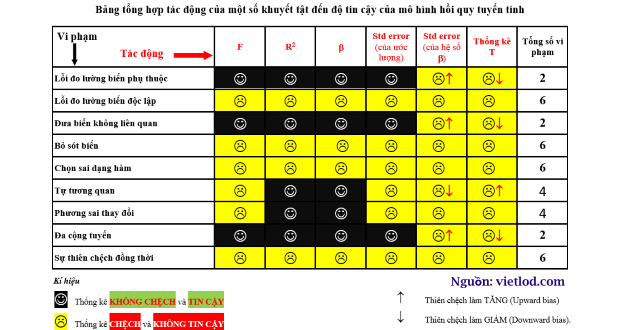
Bên cạnh các khuyết tật như đa cộng tuyến, sự tự tương quan thì một nhóm khuyết tật ảnh hưởng nghiêm trọng hoặc hoặc rất nghiêm trọng đến kết quả mô hình là đặc tả sai mô hình. Đặc tả sai mô hình là khuyết tật nghiêm trọng nhất trong phân tích kinh tế lượng. Đồng thời nó cũng là khuyết tật khó phát hiện và xử lý nhất trong phân tích kinh tế lượng.

Đặc tả sai mô hình bao gồm rất nhiều vấn đề có thể kể đến như xác định độ cong (tuyến tính hay không), dạng hàm (sử dụng hàm log, hàm mũ, hoặc hàm bình phương…) và tính chính xác trong việc đo lường biến… Những vấn đề này có ảnh hưởng nghiêm trọng đến phân tích hồi quy. Nó không chỉ là vấn đề về dữ liệu mà còn bởi mô hình được lựa chọn. Đặc tả sai mô hình có thể gồm nhiều loại như: sai dạng hàm, bỏ sót biến, hoặc lỗi đo lường biến.

3.

Sai dạng hàm

Nếu mối quan hệ đúng giữa các biến là phi tuyến nhưng bạn sử dụng mô hình tuyến tính và không thực hiện chuyển đổi các biến thì các kết quả sẽ bị chệch.

Vì sao lại như vậy?

Nguyên tắc cơ bản của ước lượng hồi quy là tìm một bộ các hệ số có thể tối thiểu hóa tổng phần dư bình phương. Phần dư chính là sự khác nhau giữa giá trị dự báo (điểm nằm trên đường hồi quy) của biến phụ thuộc so với giá trị thực trong dữ liệu. Nếu dạng hàm là không đúng thì mỗi điểm trên đường thẳng hồi quy sẽ không còn đúng bởi vì đường thẳng được dựa trên một dạng hàm không đúng.

Ví dụ qua đồ thị Scatter ta thấy Y có mối quan hệ dạng hàm log với biến X. Nếu chúng ta thực hiện hồi quy Y theo X (không phải là logX thì đường thẳng được ước lượng sẽ có sự lệch hệ thống bởi vì chúng ta đã “bẻ thẳng” một đường cong. Các phần dư, khi đó sẽ được tính toán từ một đường thẳng không đúng dẫn đến toàn bộ kết quả phân tích sẽ bị lệch.

Một số phương pháp sau để nhận diện vấn đề sai dạng hàm

• Thực hiện các kiểm tra trực quan bằng đồ thị thể hiện mối quan hệ giữa giá trị dự báo và phần dư.
• Nếu đồ thị trực quan này cho thấy có vấn đề, thực hiện các kiểm định như RESET hoặc DW để kiểm chứng.
• Kiểm tra sai phân (nếu có) của mô hình.
• Kiểm tra dạng tuyến tính thông qua đồ thị phân tán của các biến. Nếu có dạng phi tuyến thì nó có dạng nào log, bình phương…?

4.

Bỏ sót biến (Omitted variable)

Bỏ sót biến có nghĩa là những biến thực sự có vai trò giải thích cho biến phụ thuộc không có trong mô hình hồi quy. Tham khảo thêm bài hồi quy 2 giai đoạn và hồi quy biến công cụ.

Phương pháp kiểm tra bao gồm:

• Bất kì dạng đồ thị nào thể hiện đặc tả sai mô hình hoặc phương sai thay đổi đều có thể do sai dạng hàm hoặc bỏ sót biến.
• Nếu kiểm tra trực quan phát hiện vấn đề thì có thể sử dụng kiểm định RESET để kiểm chứng.
• Sử dụng các kết quả nghiên cứu trước đó, các kiến thức hoặc kinh nghiệm của chuyên gia để phát hiện biến bị bỏ sót.