Đọc kết quả ước lượng OLS – Stata
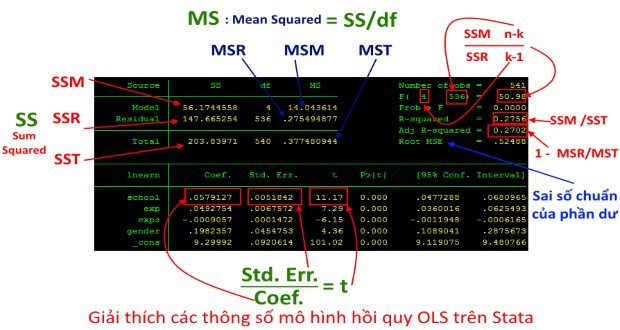
Tiếp theo bài phương pháp ước lượng hồi quy tuyến tính, bài viết này sẽ trình bày cách đánh giá độ tin cậy của mô hình và hướng dẫn đọc kết quả ước lượng OLS. Nội dung bao gồm 2 phần: đầu tiên là phần đánh giá độ tin cậy của mô hình hồi quy tuyến tính; tiếp đến là hướng dẫn đọc kết quả ước lượng OLS trên phần mềm Stata.
I.Đánh giá độ tin cậy của mô hình hồi quy tuyến tính
Khi mô hình dự báo đã được xây dựng, chúng ta có thể sử dụng các kiểm định thống kê hoặc phương pháp đồ thị để đánh giá mô hình được xây dựng có phù hợp với dữ liệu thực tế hay không. Các nội dung bên dưới sẽ trình bày kiểm định thống kê t và thống kê F để kiểm định ý nghĩa thống kê của các tham số độ dốc và mô hình.
1. Kiểm định thống kê t
Nội dung chính
Giả thuyết H0 của kiểm định thống kê t là tham số độ dốc \({\beta _1} = 0\)
Giá trị thống kê t khi đó được tính theo công thức: \(t = \frac{{{b_1} – {\beta _1}}}{{{S_{b1}}}}\)
Nếu giá trị t này lớn hơn \({t_{\alpha /2,n – k}}\) tra bảng Student với mức ý nghĩa \({\alpha /2}\) và bậc tự do n-k (ở đây k=2) thì chúng ta có thể bác bỏ giả thuyết H0 ban đầu ở mức ý nghĩa \(\alpha \). Điều đó có nghĩa tham số độ dốc ước lượng khác 0.
2. Hệ số xác định \({R^2}\)
Hệ số xác định là thước đo sự phù hợp giữa dữ liệu được giải thích bởi phương trình hồi quy và giá trị được quan sát trong dữ liệu. Trong hồi quy tuyến tính giản đơn, hệ số xác định chính là ước lượng của hệ số tương quan Pearson bình phương. Giá trị hệ số xác định càng cao thì mô hình được xây dựng càng dự đoán tốt dữ liệu hiện có và ngược lại.
Ví dụ, nếu hệ số xác định bằng 0.69 nghĩa là 69% sự thay đổi của biến giải thích trong dữ liệu đã được giải thích bởi mô hình.
Công thức tính hệ số xác định: \({R^2} = \frac{{SSM}}{{SST}}\)
Trong đó:
- \(SSM = \sum\limits_{i = 1}^n {{{({{\hat Y}_i} – \bar Y)}^2}} \): phần phương sai được giải thích bởi mô hình.
- \(SST = \sum\limits_{i = 1}^n {{{({Y_i} – \bar Y)}^2}} \): phương sai chung của mô hình
- SSR = SST – SSM: phần phương sai chưa được giải thích bởi mô hình
Như vậy, nếu \({R^2}\) = 1 có nghĩa là SSM = SST (mô hình giải thích dữ liệu 1 cách hoàn hảo). Ngược lại, nếu \({R^2}\) = 0 nghĩa là SSM = 0 hay SSR = SST (mô hình chỉ bao gồm sai số và không có khả năng giải thích).
3. Kiểm định thống kê F
Nếu giá trị của hệ số xác định tiến tới 0 sẽ dẫn đến nghi ngờ các hệ số độc lập trong mô hình hoàn toàn không có ý nghĩa trong việc mô tả đối tượng dự báo (các \({\beta _i} = 0\)). Kiểm định ý nghĩa thống kê của hệ số xác định thông qua kiểm định thống kê F sẽ được sử dụng để kiểm chứng vấn đề này.
Kiểm định thống kê F với giả thuyết H0 cho rằng tất cả các tham số độ dốc trong mô hình đều bằng 0 và giả thuyết thay thế H1 là có ít nhất 1 tham số độ dốc trong mô hình khác 0 có ý nghĩa thống kê.
Giá trị thống kê F được tính theo công thức: \(F = \frac{{SSM}}{{SST – SSM}}\frac{{n – k}}{{k – 1}}\)
Nếu giá trị thống kê F tính toán này lớn hơn giá trị thống kê F tới hạn \(F_{k – 1;n – k}^\alpha \) thì chúng ta có thể bác bỏ giả thuyết H0 trên, nghĩa là có ít nhất một tham số độ dốc khác 0 có ý nghĩa thống kê \(\alpha \)
Tuy nhiên, nếu giá trị hệ số xác định được tính theo cách trên sẽ bị lệch theo hướng lớn hơn nếu như cở mẫu nhỏ. Chúng ta có thể khắc phục vấn đề này bằng sử dụng hệ số xác định điều chỉnh như sau:
\(R_{adj}^2 = 1 – \frac{{MSR}}{{MST}} = 1 – \frac{{SSR}}{{SST}}\frac{{n – 1}}{{n – k}}\)
Ý nghĩa của hệ số xác định điều chỉnh:
Hệ số xác định điều chỉnh có ý nghĩa tương tự như hệ số xác định thông thường, tuy nhiên, lợi thế của nó là không phụ thuộc vào số tham số của mô hình. Từ đó, nó có thể sử dụng để so sánh các mô hình với số tham số khác nhau.