Điểm dị biệt – Outliers
I. ĐIỂM DỊ BIỆT LÀ GÌ?
Các điểm dị biệt (outliers) là những điểm có giá trị khác xa so với phần còn lại của dữ liệu. Việc xác định giá trị của điểm dị biệt là chủ quan. Trong khi đó, có một vài tiêu chuẩn để xác định một điểm có phải là điểm dị biệt hay không.
Có nên kiểm tra loại bỏ điểm dị biệt không?
- Các điểm dị biệt có thể làm méo mó tính chuẩn hóa của dữ liệu. Vì sự chuẩn hóa dữ liệu (phân phối chuẩn) là một trong những giả định quan trọng cho đa số các kiểm định thống kê, do vậy, chúng ta sẽ thực hiện, kiểm tra và loại bỏ ảnh hưởng của các điểm dị biệt để đưa dữ liệu về dạng chuẩn hóa. Tuy nhiên, chỉ vì những điểm dị biệt mà giá trị của chúng khác xa so với phần còn lại mà cho là dị biệt, hoặc không hợp lý hoặc nên loại bỏ thì có gì không được ổn. Hoặc việc tùy ý loại bỏ một giá trị dị biệt được khảo sát thực tế bởi vì nó không thỏa mãn giả định về tính chuẩn hóa của dữ liệu cũng là một vấn đề cần xem xét. Thực hiện nghiên cứu là nhằm mục đích khám phá thế giới thực tế. Nếu người được phỏng vấn chọn trả lời như vậy thì dữ liệu đó là một phản ánh thực tế. Vì vậy việc loại bỏ điểm dị biệt là mâu thuẫn (antithesis) với mục đích nghiên cứu của bạn.
- Điểm dị biệt được tìm thấy rất nhiều trong các nghiên cứu. Nếu bạn thực hiện kiểm tra điểm dị biệt (chẳng hạn, trên 100 biến ở các cuộc khảo sát), bạn sẽ phải kiểm tra cho tất cả các biến, và cũng như các biến tương tác giữa các biến. Với một số lượng lớn biến như vậy, bạn sẽ luôn luôn phát hiện được điểm dị biệt trong mỗi nghiên cứu. Nếu bạn tìm và loại các điểm dị biệt, theo nguyên tắc, bạn cũng nên thực hiện cùng lúc một nghiên cứu khác có tính đến các điểm dị biệt này. Rất nhiều nhà nghiên cứu không thực hiện phân tích (loại) điểm dị biệt trong các nghiên cứu của họ vì sự rối rắm và đôi khi là quá mức cần thiết. Vì vậy, nếu điểm dị biệt là các giá trị hợp lí vậy tại sao chúng ta lại phân tích (loại) tất cả chúng.
- Thông thường trong nghiên cứu người ta sử dụng nhiều câu hỏi để đo lường một khái niệm (biến). Nói một cách khác, một biến có thể được đo lường bằng một tổ hợp các câu hỏi với những trọng số cụ thể. Chẳng hạn, trong nghiên cứu về chất lượng dịch vụ thì thang đo chất lượng dịch có thể được đo lường qua 20 câu hỏi từ 5 thành phần chính như tính hữu hình, tính đáng tin cậy, khả năng đáp ứng, năng lực phục vụ và sự đồng cảm (Parasuraman, 1988). Do vậy, khi phân tích dữ liệu có thể có một bài điểm dị biệt trong mỗi câu hỏi riêng rẻ nhưng khả năng xuất hiện điểm dị biệt của thang đo chất lượng dịch vụ có thể được giảm bớt.
- Lý do cuối cùng giải thích tại sao không nên loại bỏ điểm dị biệt. Nếu bạn quyết định giảm ảnh hưởng của điểm dị biệt, như đã đề cập ở phần trên, sau đó bạn kiểm tra lại đã loại bỏ hết các điểm dị biệt chưa. Điều này đôi khi làm xuất hiện các điểm dị biệt mới bởi vì chúng đã bị che bởi các điểm dị biệt cũ hoặc sau khi loại bỏ các điểm dị biệt cũ tập dữ liệu mới sẽ tồn tại những điểm tột cùng (extreme) theo tiêu chuẩn điểm dị biệt. Quá trình này sẽ lặp lại nếu bạn tiếp tục loại bỏ những những điểm dị biệt mới.
II. CÁC LOẠI ĐIỂM DỊ BIỆT
Có hai loại điểm dị biệt – univariate (tạm dịch là dị biệt đơn lẻ) và multivariate outliers (dị biệt kết hợp)
- Univariate outliers là những giá trị tột cùng trong một biến đơn lẻ. Chẳng hạn, nếu bạn có 10 câu hỏi khảo sát trong nghiên cứu thì bạn sẽ phân tích 10 lần riêng biệt điểm dị biệt Univariate. Bạn cũng có thể thực hiện phân tích điểm dị biệt Univariate cho biến mới là trung bình của 10 câu hỏi khảo sát trên. Ngoài ra, bạn cũng có thể phân tích điểm dị biệt Univariate bên trong mỗi nhóm hoặc nhóm đối tượng thỏa mãn điều kiện lọc. Ví dụ, bạn có thể phân tích Univariate của 10 câu hỏi trên trong mỗi nhóm đối tượng theo giới tính (nam, nữ); nhóm tuổi; khu vực (thành thị, nông thôn) hoặc nhóm đối tượng là nữ ở khu vực nông thôn…
- Multivariate outliers là những giá trị tột cùng kết hợp của 2 hay nhiều biến biến. Chẳng hạn, nếu bạn muốn xem xét mối quan hệ giữa chiều cao và cân nặng thì có những kết hợp của 2 biến này có giá trị tột cùng so với các kết hợp còn lại. Đó có thể là những kết hợp cao nhưng cân nặng hoặc cao nhưng nhẹ cân, cao và nặng …
Đầu tiên, bạn nên quan tâm đến điểm dị biệt Univariate và tiếp đến là điểm dị biệt Multivariate
2.Điểm dị biệt Unvariate
Kiểm tra điểm dị biệt Univariate không phân theo nhóm (Sử dụng filePhân tích dữ liệu)
- Chọn Analyze –> Descriptive Statistics –> Explore
- Chuyển tất cả các biến liên tục vào cửa sổ “Dependent List:“. Lưu ý rằng điểm dị biệt không bao gồm các biến có dạng chuỗi.
- Bấm “Statistics“, và chọn là “Outliers“
- Bấm “Plots“, và bỏ chọn mục “Stem-and-leaf“.
- Bấm OK.
Kết quả phân tích điểm dị biệt Unvariate cho biến “system1”

Bảng “Descriptives” cho biết kết quả thống kê mô tả của biến, bao gồm giá trị độ trôi (Skewness) và độ nhọn (Kurtosis), đi kèm với sai số chuẩn của mỗi chỉ số. Thông tin này sẽ hữu ích khi đề cập đến vấn đề tính chuẩn hóa của dữ liệu. “5% Trimmed Mean” cho biết giá trị trung bình sau khi loại bỏ 5% giá trị cao nhất và thấp nhất của biến. Bằng cách so sánh chỉ số này (5% Trimmed Mean) với giá trị trung bình (mean), bạn có thể xác định xem có các giá trị tột cùng có ảnh hưởng đến biến không.
Bảng “Extreme Values” và đồ thị Boxplot có mối liên quan với nhau.

Đồ thị boxplot là một dạng đồ thị cho biết một số thông tin về dữ liệu như: (1) giá trị trung vị (median), đó là đường thẳng màu đen ở giữa, (2) khoảng 50% điểm giữa, đó là hộp được tô màu ở giữa, (3) điểm phân vị 25% và 75%, đó là các đường nằm ngang phía trên và dưới kéo dài của hộp được tô màu, (4) điểm cao nhất và thấp nhất (không phải điểm dị biệt), đó là các đường nằm ngang trên cùng và dưới cùng của đồ thị và (5) các điểm dị biệt. Đồ thị boxplot thể hiện cả điểm dị biệt cứng (mild outliers) và điểm dị biệt cực mạnh (extreme outilers).

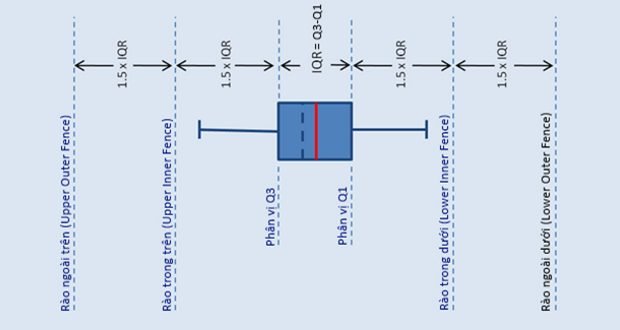
Điểm dị biệt cứng được thể hiện là những dấu chấm tròn (o) kèm theo là vị trí của quan sát. Đó là những điểm có giá trị chênh lệch 1,5 lần khoảng phân vị so với điểm phân vị 25% và 75%. Điểm dị biệt cực mạnh có giá trị chênh lệch 3 lần khoảng phân vị và được thể hiện là những dấu sao (*). Cụ thể, các điểm dị biệt này được tính như hình bên dưới

Công thức xác định điểm dị biệt trong tập dữ liệu:
- Upper outer fence (UOF) = Q3 + 3*IQ
- Lower outer fence (LOF) = Q1 – 3*IQ
Trong đó:
- Q1, Q3 lần lượt là các phân vị 25% và 75%
- IQ = Q3 – Q1 được gọi khoảng bên trong phân vị
- Các quan sát có giá trị nằm ngoài UOF và LOF được xem là các điểm dị biệt cực mạnh.
- Các quan sát có giá trị nằm ngoài UIF và LIF được gọi là các dị biệt cứng.
Điểm dị biệt trong mỗi nhóm
Một cách khác để phát hiện điểm dị biệt univariate là thực hiện kiểm tra điểm dị trên trong các nhóm khác nhau. Chẳng hạn, kiểm tra giá trị dị biệt của một biến định lượng ở mỗi nhóm nam/nữ. Quá trình này được thực hiện như sau:
- Chọn Analyze –> Descriptive Statistics –> Explore
- Chuyển tất cả các biến liên tục vào cửa sổ “Variable(s)“.
- Chuyển biến phân loại “sex” vào ô “Factor List“
- Bấm “Statistics“, và chọn “Outliers“
- Bấm “Plots“, và bỏ chọn “Stem-and-leaf“
- Bấm OK.
Kết quả phân tích điểm dị biệt trong mỗi nhóm (sex) đối với “system1”

Bảng “Descriptives” cho biết thống kê mô ta cho biến. Lưu ý rằng, các thông tin mô tả của biến sẽ được thể hiện riêng biệt.
Bảng “Extreme Values” và đồ thị Boxplot có mối quan hệ với nhau. Lưu ý rằng sự khác nhau của mỗi nhóm.


Điểm dị biệt Multivariate
Điểm dị biệt Multivariate là sẽ được đề cập khi thực hiện phân tích tương quan và phân tích hồi quy. Phân tích điểm dị biệt multivariate khá phức tạp và sẽ được trình bày kĩ hơn ở phần tương quan và hồi quy.