Kiểm định Friedman – Stata
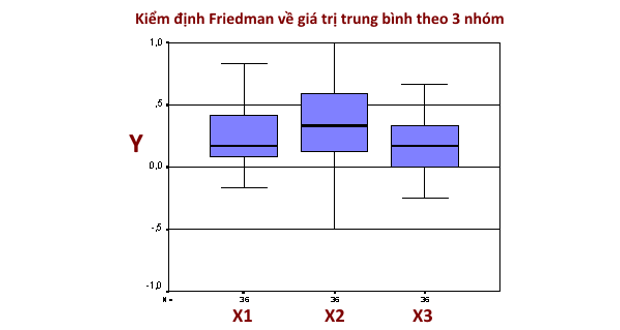
Kiểm định Friedman là một kiểm định phi tham số được sử dụng thay thế kiểm định ANOVA lặp một chiều. Kiểm định Friedman được sử dụng khi muốn kiểm tra sự khác nhau về giá trị trung bình giữa các nhóm khi biến phụ thuộc được đo lường là dạng thứ tự. Nó cũng có thể được sử dụng trong trường hợp biến phụ thuộc (dạng liên tục) vi phạm các giả định cần thiết của kiểm định ANOVA lặp một chiều, đặc biệt là, giả định về phân phối chuẩn.
Xem thêm: Kiểm định phi tham số
Ví dụ: Để tìm hiểu tâm lý mua sắm của người tiêu dùng trong mảng điện thoại cao cấp (Smart phone), giám đốc kinh doanh của hệ thống A thực hiện chương trình như sau ở 25 cửa hàng trong hệ thống:
- Tuần 1: bán hàng đúng giá niêm yết
- Tuần 2: bán hàng có chiết khấu (giảm giá) 5% trực tiếp trên những hóa đơn trên 8 triệu.
- Tuần 3: bán hàng có quà tặng (tương ứng giá trị 5%) cho những hóa đơn trên 8 triệu.
Số liệu thu thập từ 25 cửa hàng được thể hiện trong file dữ liệu thực hành là friedman.dta
use https://www.vietlod.com/data/friedman.dta, clear
Trong trường hợp này, biến phụ thuộc là số lượng điện thoại bán ra ở từng cửa hàng (chiếc điện thoại/tuần) và biến độc lập là chương trình thực hiện (bao gồm 3 chương trình: bán bình thường, bán có chiết khấu, và bán kèm theo quà tặng). Các biến này thể hiện trong dữ liệu lần lượt là none, discount và gift.
Câu hỏi vị giám đốc này đặt ra là số lượng điện thoại bán ra ở các cửa hàng trong mỗi chương trình có khác nhau không?.
Thông tin chung về dữ liệu được mô tả bằng như bên dưới:
su none discount gift

Doanh số bán hàng trung bình của 25 cửa hàng ở 3 chương trình bình thường (none), giảm giá (discount) và tặng quà (gift) là 43.32; 46.84 và 47.88 chiếc/tuần. Để kiểm tra số lượng điện thoại bán ra ở các cửa hàng trong mỗi chương trình có khác nhau không chúng ta có thể sử dụng phương pháp ANOVA lặp 1 chiều hoặc kiểm định Friedman.
Trước khi sử dụng kiểm định ANOVA lặp 1 chiều hay kiểm định Friedman, chúng ta cần kiểm tra dạng phân phối của của các biến liên tục để quyết định loại kiểm định nào là phù hợp.
Kết quả kiểm tra phân phối chuẩn bằng cách sử dụng các lệnh pnorm, qnorm lần lượt với các biến liên tục cho thấy các biến này đều có sự lệch so với phân phối chuẩn.
