Kiểm định tham số-phi tham số

Có hai loại kiểm định: kiểm định tham số (Parametric tests) và kiểm định phi tham số (Nonparametric tests).
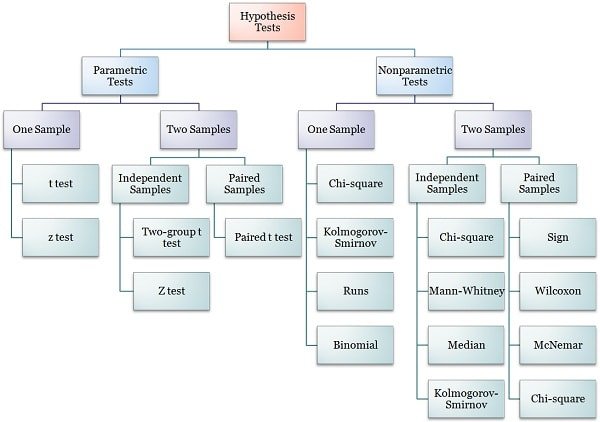
1. KIỂM ĐỊNH THAM SỐ
Kiểm định tham số (Parametric tests) là công cụ mạnh vì xử lý các dữ liệu dạng scale (interval, ratio). Thực hiện kiểm định này đòi hỏi một số giả định:
- Các quan sát phải độc lập với nhau,
- Các quan sát phải được rút ra từ các tổng thể có phân phối chuẩn,
- Các tổng thể nên có phương sai đồng nhất,
- Thang đo phải ở dạng scale để các tính toán có thể thực hiện được.
Ưu điểm của kiểm định tham số là đơn giản, dễ thực hiện, độ tin cậy cao. Tuy nhiên, nó đòi hỏi khắt khe về sự “chuẩn hóa” của dữ liệu. Do vậy, chi phí thu thập (thực hiện) cao và đôi khi khó thực hiện trong thực tế.
Ví dụ: Chúng ta muốn so sánh lương khởi điểm của sinh viên tốt nghiệp ở ngành kinh tế và điện tử. Thu nhập dữ liệu từ 200 doanh nghiệp trên địa bàn TpHCM, chúng ta kiểm định giả thuyết là lương khởi điểm của sinh viên tốt nghiệp ở 2 ngành này là như nhau.
Mỗi kiểm định tham số đều có tương ứng một kiểm định phi tham số thay thế. Chẳng hạn, kiểm định Kruskal–Wallis thay thế phân tích phương sai một chiều, kiểm định dấu và hạng Wiloxon sử dụng thay thế kiểm định t-test cặp đôi hoặc hạng tương quan Spearman thay thế hồi quy tuyến tính… Một số kiểm định thay thế này được liệt kê ở bảng bên dưới.
2. KIỂM ĐỊNH PHI THAM SỐ
Trong nhiều tình huống thực tế, số liệu chỉ có thể biểu hiện dưới hình thức dấu hoặc xếp hạng, vì vậy không thể sử dụng các kiểm định tham số để thực hiện. Trong trường hợp này kiểm định Wilconxon và Mann-Whitney là hai lọai kiểm định phi tham số thông dụng nhất ứng với hai trường hợp: một là sử dụng cho mẫu ngẫu nhiên gồm các quan sát từng cặp và một dùng cho mẫu ngẫu nhiên độc lập.
Kiểm định phi tham số (Nonparametric Tests) được sử dụng trong những trường hợp dữ liệu không có phân phối chuẩn, hoặc cho các mẫu nhỏ có ít quan sát. Kiểm định phi tham số cũng được dùng cho các dữ liệu định danh (nominal), dữ liệu thứ bậc (ordinal) hoặc dữ liệu khoảng cách (interval) có phân phối bất kì.
Nhược điểm của kiểm định phi tham số là khả năng tìm ra được sự sai biệt kém, không mạnh như các phép kiểm có tham số (T student, phân tích phương sai…), đồng thời khó mở rộng để giải quyết các mô hình kinh tế phức tạp.
Sau đây là các kiểm định phi tham số được dùng tương đương với các kiểm định có tham số.
Bảng 1: Tổng hợp các kiểm định phi tham số và kiểm định tham số
| Kiểm định phi tham số (Non-parametric statistics) | Kiểm định tham số (Parametric statistics) |
| Chi-square \({\chi ^2}\) | |
| Multiway Frequency Analysis \({\chi ^2}\) | |
| Spearman Rank Order Correlation \({r_S}\) | Pearson Product Moment Correlation \({r_P}\) |
| Mann-Whitney U | Independent-samples t |
| Wilcoxon Signed Rank | Paired-samples t |
| Kruskal-Wallis H | One-way between-groups ANOVA F |
| Friedman | Two-way repeated-measures ANOVA F |
| ANCOVA, MANOVA | |
| Regression analysis R | |
| Bayesian dependency modeling (B-Course) | Exploratory factor analysis – EFA |
| Principal component analysis – PCA | |
| Cluster analysis | |
| Logit, Probit, Tobit regression | Discriminant analysis |
| Bayesian classification modeling (B-Course) | Classification analysis |
| Categorical variable modeling (Mplus) | Confirmatory factor analysis – CFA |