Khuynh hướng phân tán của dữ liệu
1. Giới thiệu về khuynh hướng phân tán của dữ liệu
Để biết xu hướng tập trung của dữ liệu ta dùng các tham số như Mean, Median, Mode. Tuy nhiên, một câu hỏi quan trọng nữa cần phải trả lời khi xem xét một chất lượng của mẫu là “làm sao đo lường sự biến thiên (hay sự phân tán) của dữ liệu trong mẫu?” Vì có thể 2 mẫu có cùng trung bình nhưng sự biến thiên của dữ liệu là khác nhau. Bài viết sau sẽ tiếp tục bài khuynh hướng tập trung của dữ liệu trình bày về khuynh hướng phân tán của dữ liệu.
Các tính toán minh họa đều sử dụng ví dụ minh họa ở bài đo lường khuynh hướng tập trung của dữ liệu
2. Đo lường khuynh hướng phân tán của dữ liệu
Để đo lường khuynh hướng phân tán của dữ liệu người ta thường dùng các tham số phạm vi (Range), Khoảng tứ phân vị (IQR), độ lệch chuẩn (Standard deviation), phương sai (Variance) và sai số chuẩn (Standard Error). Chúng ta lần lượt trình bày các vấn đề trên, bắt đầu với thuật ngữ khoảng phân vị
1.Tứ phân vị (IQR)
Tứ phân vị là đại lượng mô tả sự phân bố và sự phân tán của tập dữ liệu. Tứ phân vị có 3 giá trị, đó là tứ phân vị thứ nhất (Q1), thứ nhì (Q2), và thứ ba (Q3). Ba giá trị này chia một tập hợp dữ liệu (đã sắp xếp dữ liệu theo trật từ từ bé đến lớn) thành 4 phần có số lượng quan sát đều nhau.
Tứ phân vị được xác định như sau:
– Sắp xếp các số theo thứ tự tăng dần
– Cắt dãy số thành 4 phàn bằng nhau
– Tứ phân vị là các giá trị tại vị trí cắt
Khoảng tứ phân vị (Interquartile Range – IQR). IQR được xác định bằng giá trị Q3 – Q1
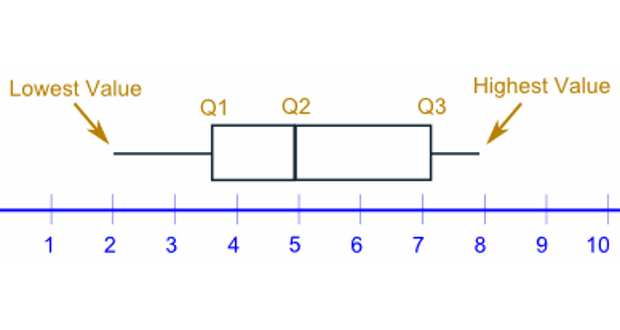
Box Plot (Biểu đồ hộp)
Box Plot giúp bạn biểu diễn các đại lượng quan trọng của dãy số như Min, Max, Quartile, IQR một cách trực quan, dễ hiểu. Một Box plot có dạng như sau:
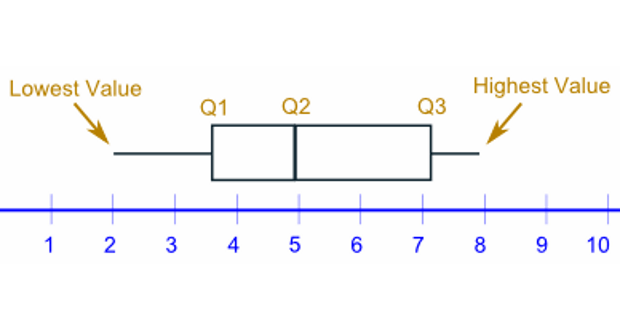
Ví dụ: sử dụng Box plot để biểu diễn các tham số quan trọng của dữ liệu. Giả sử có dãy số như sau: 4, 17, 7, 14, 18, 12, 3, 16, 10, 4, 4, 11
- Sắp xếp dữ liệu: 3, 4, 4, 4, 7, 10, 11, 12, 14, 16, 17, 18
- Xác định tứ phân vị: 3, 4, 4 | 4, 7, 10 | 11, 12, 14 | 16, 17, 18
- Quartile 1 (Q1) = (4+4)/2 = 4
- Quartile 2 (Q2) = (10+11)/2 = 10.5
- Quartile 3 (Q3) = (14+16)/2 = 15
Xác định Min, Max
- Min = 3
- Max = 18
Bây giờ đã có đủ dữ liệu để vẽ Box plot như sau:

Nguồn: http://bis.net.vn/forums/t/489.aspx
Và khoảng phân vị (IQR) = Q3 – Q1 = 15 – 4 = 11
Còn tiếp…