Hồi quy logit chính xác – Exact Logit

Lựa chọn phương pháp phân tích

• Hồi quy logit chính xác – Đây là một phương pháp phân tích phù hợp bởi biến phụ thuộc có dạng nhị phân, cở mẫu nhỏ và một vài ô trong bảng tần suất ít quan sát.
• Hồi quy logit thông thường – Do cở mẫu nhỏ và sự hiện diện của một số ô trống (không đủ dữ liệu) do vậy, hồi quy logit với ước lượng hợp lý cực đại sẽ không thực hiện được.
• Bảng ngẫu nhiên 2 chiều: Bạn sử dụng tùy chọn exact để tính giá trị kiểm định Fisher’s exact cho các giá trị kì vọng nhỏ.

Bài viết này sẽ trình bày minh họa phương pháp hồi quy logit chính xác để giải quyết vấn đề được nêu ra trong ví dụ

Minh họa hồi quy logit chính xác

Sử dụng lệnh exlogistic trên STATA để phân tích hồi quy logit chính xác. Chúng ta sử dụng tùy chọn coef để hiển thị kết quả các hệ số ước lượng dạng log của odds thay vì các hệ số dạng odds ratios (hệ số được mũ hóa). Chúng ta sử dụng trọng số tần suất trong câu lệnh exlogistic như sau:

exlogistic admit female apcalc [fw=num], coef

Đầu tiên là phần kết quả quá trình nhân bản đối tượng, cho biết có bao nhiêu trường hợp xảy ra khi mỗi quan sát được xử lí. Chẳng hạn, đối với quan sát 6 có 536 sự kết hợp riêng rẻ của female và apcalc trong tổng số các trường hợp. Quá trình chỉ liệt kê 7 quan sát. Điều này bởi vì chúng ta chỉ có 8 dòng trong tập dữ liệu, trong đó 1 dòng có giá trị đếm (biến num) bằng 0. Chúng ta sử dụng biến num là biến trọng số tần suất để mở rộng số quan sát lên 30.

Phần kết quả ở khung bên phải cho biết số quan sát được sử dụng trong phân tích. Ở đây chúng ta có 30 quan sát được sử dụng. Chúng ta cũng thấy rằng mô hình chung là có ý nghĩa thống kê. Kiểm định sự phù hợp của mô hình được thể hiện ở dòng Model score = 13.8 với mức ý nghĩa 0.0005 cho thấy mô hình có ý nghĩa thống kê. Giá trị của Model score chính là giá trị kiểm định Chi2.

Trong bảng kết quả hệ số, cho biết các hệ số ước lượng, giá trị thống kê (Suff), mức ý nghĩa 2*Pr(Suff.), và khoảng tin cậy 95% của hệ số. Thống kê Suff kiểm tra giả thuyết cho rằng hệ số của biến bằng 0. Các giá trị mức ý nghĩa và khoảng tin cậy được tính từ các phân phối xác suất có điều kiện.

Lưu ý: không giống như hồi quy logit thông thường, trong hồi quy logit chính xác mỗi biến giải thích được ước lượng riêng biệt so với những biến giải thích khác.

Kết quả cho thấy biến female không có ý nghĩa thống kê. Ý nghĩa của hệ số ước lượng biến apcalc được giải thích như sau: thay đổi 1 đơn vị trong biến apcalc thì giá trị kì vọng log của odds cho biến admit sẽ tăng 3.34.

Chúng ta cũng ước lượng hệ số của odds ratios bằng cách bỏ tùy chọn coef trong câu lệnh trên như sau:

exlogistic admit female apcalc [fw=num]

Chúng ta có thể diễn giải kết quả này như sau: những học sinh đã tham gia chương trình AP (apcalc=1) sẽ có odds cao hơn 28.2 lần so với những học sinh không tham gia chương trình AP (apcalc=0).

Chúng ta cũng có thể tính toán các sai số chuẩn của odds ratio bằng câu lệnh estat như sau:

estat se

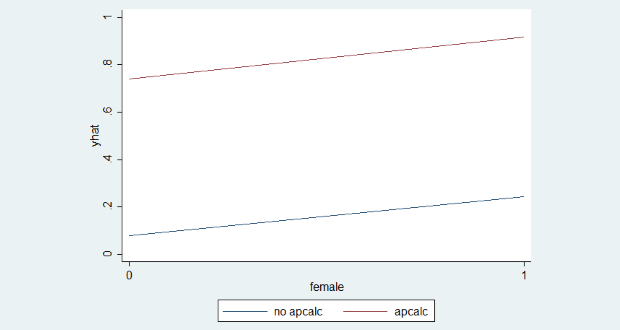
Đồ thị xác suất dự đoán của biến phụ thuộc theo các mức giá trị của biến giải thích (female và apcalc) được thể hiện như sau:

GHI CHÚ:

1. Dữ liệu bị phân riêng từng phần hoặc hoàn hảo xảy ra khi giá trị của biến phụ thuộc Y chỉ có 1 giá trị ứng với một khoảng giá trị (từng phần) hoặc toàn bộ giá trị (hoàn hảo) của biến liên tục độc lập X. Chẳng hạn với tập dữ liệu như sau:
Y      X1      X2
0       1          3
0       2          2
0       3         -1
0       3         -1
1        5         2
1        6         4
1       10        1
1       11        0

Chúng ta dễ dàng quan sát thấy Y sẽ luôn bằng 0 ứng với giá trị của X1 nhỏ hơn 3. Hoặc Y luôn bằng 1 khi X1 lớn hơn 3. 2 vấn đề này được gọi là hiện tượng phân riêng từng phần. Trong trường hợp này không cần hồi quy logit chúng ta cũng có thể dự đoán chính xác giá trị của Y theo giá trị của X1. Với dữ liệu như vậy, chúng ta luôn có: Prob(Y = 1 | X1<=3) = 0 and Prob(Y=1 X1>3) = 1.