Hồi quy Logit – STATA
Giới thiệu về hồi quy logit
Hồi quy logit, đôi khi còn được gọi là mô hình logit, được sử dụng để ước lượng mô hình có biến phụ thuộc dạng nhị phân. Phương trình hồi quy logit giản đơn có dạng như sau:
\(odds({y_i} \ne 0) = \exp({b_0} + b{x_i})\)
1.Một số khái niệm liên quan đếnn hồi quy logit
- Odds của một sự kiện được tính bằng \(odds = \frac{p}{{1 – p}}\), với p là xác suất xảy ra sự kiện đó.
- Ở mức xác suất thấp (p nhỏ) thì odds tiến gần đến p. Đôi khi, các nhà dịch tể học bỏ qua khái niệm chính thống của odds mà xem odds như là một risk. Điều này chỉ hợp lí khi odds xấp xỉ p khi p nhỏ hơn rất nhỏ.
- Tỉ lệ odds (odds ratios) hay còn được gọi là hệ số được mũ hóa (exponentiated coefficients) được định nghĩa là:
\(odds ratios = \frac{{P(event|x + 1)/(1 – P(event|x + 1))}}{{P(event|x)/(1 – P(event|x))}}\)
Hay nói cách khác tỉ lệ odds chính là tỉ số của odds khi giá trị của biến tăng thêm 1 đơn vị so với odds ban đầu.
- Tương tự như sự khác nhau giữa odds và risks thì odds ratio và risks ratio là 2 khái niệm khác nhau. Risks ratio chỉ xấp xỉ Odds ratio khi giá trị p nhỏ. Chúng ta có thể phân biệt odds ratio với risks ratio ví dụ sau:
Giả sử, kí hiệu p = P(event|x) và q = P(event|x+1)
Khi đó: Odds ratio (or) = (q/((1-q))/(p/(1-p))
Với giá trị p và or cho trước thì q = c/(1+c), với c = or*p(1-p) thay vào biểu thức q/p thì ta có Risks ratio (rr)
Kết quả thực sự của risks ratio theo các giá trị p và odds ratio được thể hiện ở bảng bên dưới:
| P(event|x) | 0.25 | 0.50 | 0.75 | 1.00 | 1.50 | 2.00 | 4.00 |
| 0.2 | 0.2941 | 0.5556 | 0.7895 | 1.000 | 1.364 | 1.667 | 2.500 |
| 0.1 | 0.2702 | 0.5263 | 0.7692 | 1.000 | 1.429 | 1.818 | 3.077 |
| 0.01 | 0.2519 | 0.5025 | 0.7519 | 1.000 | 1.493 | 1.980 | 3.883 |
| 0.001 | 0.2502 | 0.5003 | 0.7502 | 1.000 | 1.499 | 1.998 | 3.988 |
| 0.0001 | 0.2500 | 0.5000 | 0.7500 | 1.000 | 1.500 | 2.000 | 3.999 |
Nhận xét: giá trị p càng nhỏ thì risks ratio càng gần với odds ratio.
Xem thêm: hồi quy logit giản đơn trên SPSS
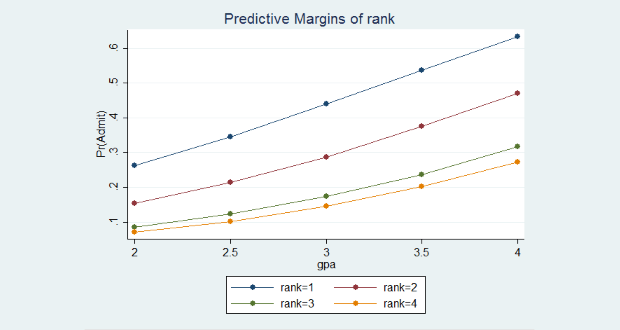
Trở lại vấn đề hồi quy logit, giả sử chúng ta muốn biết các biến như điểm bài thi cuối khóa (gre), học lực trung bình (gpa) và uy tín của trường THCS (rank) mà các học sinh theo học ảnh hưởng như thế nào đến kết quả xét tuyển (admit) ở bậc học PTTH. Biến kết quả ở đây là một biến nhị phân (được chấp nhận/không chấp nhận).
Phần minh họa sử dụng dữ liệu thực hành là binary.dta
use https://www.vietlod.com/data/binary.dta, clear
Bộ dữ liệu bao gồm 400 quan sát với 3 biến giải thích (gpa, gre, rank) và 1 biến phụ thuộc dạng nhị phân (admit). Trong 3 biến giải thích, 2 biến liên tục và một biến (rank) dạng thứ tự (nhận giá trị từ 1 đến 4). Kết quả thống kê mô tả các biến được thể hiện như bên dưới:
summarize gre gpa
tab admit rank

Xem tiếp lựa chọn phương pháp ở trang 2 và giải thích kết quả hồi quy logit ở trang 3