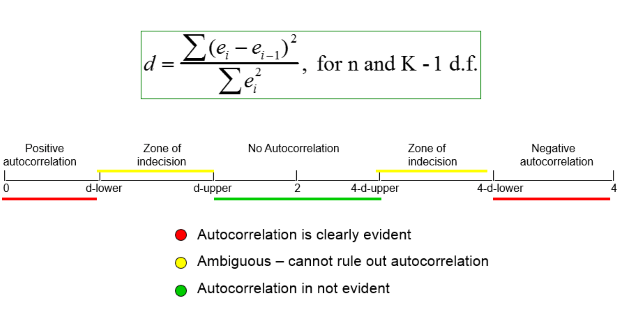
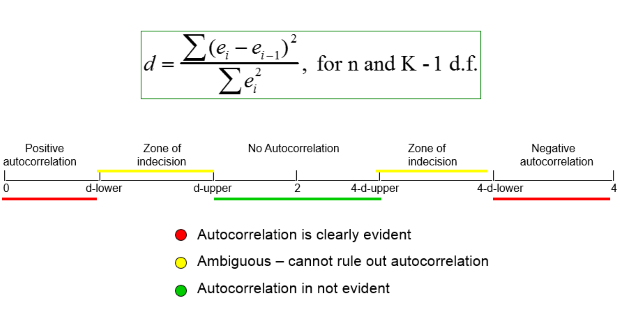
Tra cứu sự tự tương quan

Sau khi chạy hồi quy, có thể sử dụng câu lệnh dwstat để có được giá trị thống kê Durbin-Watson tính toán (dw). Kết quả của dw sẽ được so sánh với các giá trị dL, dU tra bảng (ở mức ý nghĩa alpha và số biến giải thích trong mô hình). Các giá trị này được tổng hợp ở bảng bên dưới, cụ thể như sau:

Kiểm định thống kê Durbin-Watson là một loại kiểm định được sử dụng phổ biến để phát hiện vấn đề tự tương quan trong mô hình tự hồi quy bậc 1.

Vietlod đã tổng hợp ra 2 bộ bảng tra theo Savin & White (1977) và Farebrother (1980). Bảng A.1 và A.2 được trình bày theo Savin & White (1977) cho phép tra với cở mẫu từ 6 đến 200 cùng với hệ số cắt và 1 đến 20 biến giải thích trong mô hình. Bảng A.3; A.4 tra theo Farebrother (1980) cho phép tra với cở mẫu từ 2 đến 200 và 0 đến 21 biến giải thích trong mô hình (không có hằng số cắt) với sự tự tương quan dương và Bảng A.5; A.6 cho phép tra với sự tự tương quan âm.

Hướng dẫn cách tra dL, dU, d

Bước 1

Chọn một mức ý nghĩa cho kiểm định và tra bảng các giá trị tới hạn dL và dU tại các bảng từ A.1 đến A.6 trong Ramanathan, với

• n là số quan sát,
• k’ là số biến bên vế phải của phương trình hồi quy (không bao gồm hằng số).

Trong ví dụ trên, giả sử mức ý nghĩa 5%, với n = 37, k’ = 2 thì các giá trị tới hạn tra bảng là: dL = 1.36, dU = 1.59.

Bước 2

So sánh giá trị tính toán của kiểm định thống kê Durbin-Watson với giá trị tra bảng.

• Nếu d < dL thì bác bỏ giả thuyết không và kết luận rằng có sự tự tương quan bậc 1. Nếu d > dU thì chấp nhận giả thuyết không và kết luận rằng không có sự tự tương quan bậc 1.
• Nếu dL < d < dU chưa thể kết luận.