Mô hình tác động ngẫu nhiên – RE

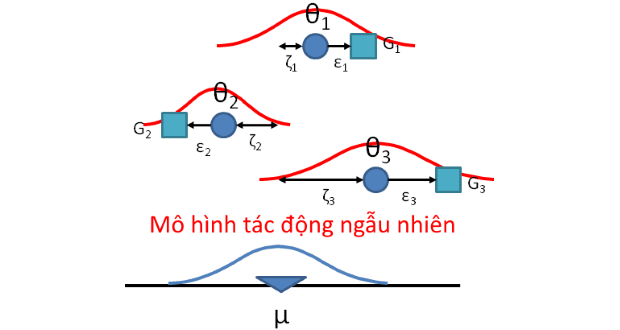
Bên cạnh mô hình tác động cố định, mô hình tác động ngẫu nhiên (Random Effect) là một trong hai mô hình được sử dụng phổ biến trong ước lượng các dữ liệu bảng. Bài viết này sẽ đi sâu trình bày mô hình tác động ngẫu nhiên, với các nội dung cụ thể như sau: Đặc điểm của mô hình Phương pháp ước lượng Các kiểm định trong mô hình Tác động thời gian của mô hình Xem thêm các bài phát hiện và xử lý các khuyết tật của mô hình hồi quy I. ĐẶC ĐIỂM MÔ HÌNH TÁC ĐỘNG NGẪU NHIÊN Xét một mối quan hệ kinh …