Sai lầm loại I – Sai lầm loại II
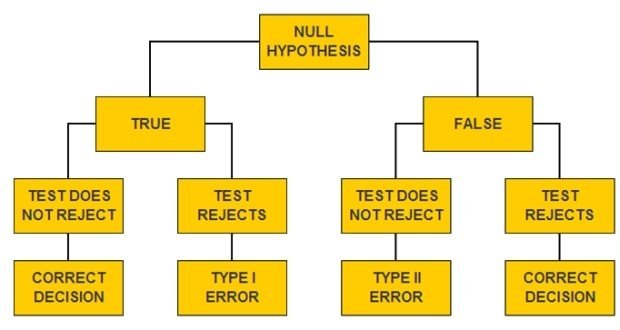
III. MINH HỌA SAI LẦM LOẠI I – SAI LẦM LOẠI II
Sai lầm loại I – sai lầm loại II có thể được minh họa qua ví dụ sau:
Cơ quan quản lý thị trường (FTC) thực hiện một cuộc kiểm tra những tiêu chuẩn đăng ký cho những sản phẩm của các nhà sản xuất. Chẳng hạn, trên bao bì túi cà phê của công ty ABC đăng ký là 3 lbs. Trong trường hợp này, giả thuyết mà các nhà quản lý thị trường (FTC) về trọng lượng đăng ký là: trung bình của tổng thể (các sản phẩm túi cà phê của ABC) bằng 3 lbs như cam kết chất lượng của ABC. Sau đó, FTC tiến hành thu thập 36 mẫu túi cà phê của ABC được chọn và giá trị trung bình mẫu được sử dụng để ước lượng giá trị trung bình của tổng thể \(\mu \). Nếu giá trị trung bình mẫu nhỏ hơn 3 lbs thì FTC có quyền nghi ngờ về giả thuyết H0. Sai lầm loại I (cáo buộc ABC vi phạm tiêu chuẩn trọng lượng đăng ký) sẽ xảy ra khi bác bỏ giả thuyết H0 ở mức ý nghĩa \(\alpha \) được chọn. Như vậy, việc lựa chọn mức ý nghĩa để kiểm định tùy thuộc vào quyết định của người kiểm tra. Nếu chi phí để phạm phải sai lầm loại I này cao thì cần chọn giá trị \(\alpha \) nhỏ và ngược lại. Trong trường hợp này, để răn đe tình trạng vi phạm tiêu chuẩn trọng lượng cam kết, FTC chọn mức ý nghĩa \(\alpha \) = 0.01
Ở hình (a), nếu FTC chấp nhận giả thuyết H0 cho rằng trọng lượng trung bình của mỗi túi cà phê của công ty ABC nhỏ hơn hoặc bằng 3 lbs thì có khả năng mắc sai lầm loại I chính là phần diện tích màu đỏ (ứng với mức ý nghĩa 5%). Độ tin cậy trong trường hợp chấp nhận H0 chính là phần diện tích 1 – \(\alpha \) = 0.95 (hay 95%) như hình bên dưới.

Hoặc nếu, nhà nghiên cứu bác bỏ giả thuyết H0 thì khả năng mắc sai lầm loại II chính là phần diện tích màu vàng kết hợp với màu xanh (tương ứng với mức ý nghĩa \(\beta \)). Độ tin cậy trong trường hợp này là phần diện tích 1 – \(\beta \) trên hình.
Điều này cũng tương tự cho ở hình (b) với mức ý nghĩa 1%. Qua đó, ta thấy mức ý nghĩa càng nhỏ thì độ tin cậy của việc chấp nhận H0 càng cao, xác suất mắc sai lầm loại I (H0 sai nhưng chấp nhận) càng thấp. Tuy nhiên, khả năng mắc sai lầm loại II (H0 đúng mà bác bỏ) cũng tăng tương ứng. Do vậy, vấn đề lựa chọn mức ý nghĩa \(\alpha \) thích hợp cho nghiên cứu là làm sao để phần diện tích màu xanh dương trên hình là nhỏ nhất.
BÀN LUẬN VỀ SAI LẦM LOẠI I – SAI LẦM LOẠI II
Giá trị anpha bằng bao nhiêu là phù hợp?
Bên cạnh về vấn đề chi phí khi mắc phải các loại sai lầm, thông thường trong các nghiên cứu thực nghiệm, tùy thuộc vào mục đích của nghiên cứu là phát hiện vấn đề, củng cố vấn đề hoặc nâng cao hiệu quả dự báo mà nhà nghiên cứu chọn mức ý nghĩa \(\alpha \) thích hợp.
Đối với các nghiên cứu khám phá, mức ý nghĩa \(\alpha \) thường cao (khoảng 10%) nhằm phác thảo tổng thể các yếu tố có thể ảnh hưởng đến đối tượng nghiên cứu. Từ các kết quả của nghiên cứu khám phá này, các nhà nghiên cứu tiếp tục phân tích sâu hơn để tìm ra những yếu tố mới hoặc củng cố các yếu tố thực sự có tác động đến đối tượng nghiên cứu bằng cách chọn một mức ý nghĩa thấp hơn (5% chẳng hạn). Mức ý nghĩa 1% có thể là một lựa chọn phù hợp cho mục đích nâng cao hiệu quả của các kết quả được dự báo.