Sai lầm loại I – Sai lầm loại II
I. GIỚI THIỆU VỀ SAI LẦM LOẠI I – SAI LẦM LOẠI II
Đối với bất kỳ một thủ tục kiểm định nào có thể xảy ra ba trường hợp sau: (1) quyết định đúng được thực hiện (nghĩa là chấp nhận giả thuyết đúng và bác bỏ giả thuyết sai), (2) giả thuyết đúng bị bác bỏ, (3) giả thuyết sai được chấp nhận.
Sai lầm bác bỏ giả thuyết H0 khi nó đúng được gọi là sai lầm loại I. Sai lầm không bác bỏ giả thuyết H0 khi nó sai được gọi là sai lầm loại II. Tương ứng với mỗi loại sai lầm này là một giá trị xác suất. Chúng được gọi là các xác suất sai lầm loại I – sai lầm loại II và được ký hiệu là \(\alpha \) và \(\beta \).
II. SAI LẦM LOẠI I – SAI LẦM LOẠI II VÀ GIẢ THUYẾT THỐNG KÊ
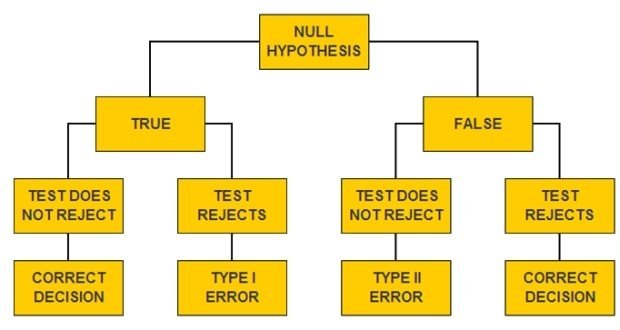
Quá trình ra quyết định lựa chọn giả thuyết và khả năng mắc phải của các loại sai lầm được thể hiện ở quy trình sau:

Tóm lại:
Khi chúng ta bác bỏ một giả thuyết là ta có thể mắc phải sai lầm loại I, còn khi ta chấp nhận một giả thuyết là ta có thể phạm phải sai lầm loại II.
Thực chất sai lầm loại I và sai lầm loại II chỉ mang tính chất tương đối. Nó được xác định khi ta đặt giả thuyết H0. Giả thuyết H0 được phát biểu chính là vấn đề hoặc câu hỏi nghiên cứu cần được giải quyết. Do vậy, trong thống kê người ta quy ước rằng sai lầm loại I (giả thuyết đúng nhưng bác bỏ) là tai hại và cần tránh trước.
Ví dụ:
- Dựa vào các thông tin dự báo thời tiết, trung tâm khí tượng thủy văn dự báo một cơn bão sắp đến sẽ đổ bộ vào miền Nam thì H0: “Bão đổ bộ vào miền Nam” (H1: bão không đổ bộ vào miền Nam). Khi đó sai lầm loại I là rất tai hại vì khi đó, do không kịp thời chuẩn bị ứng phó nên bão sẽ gây ra những thiệt hại nặng nề.
- Cho đậu một thí sinh yếu kém (sai lầm loại II) hoặc cho rớt 1 thí sinh giỏi (sai lầm loại I) đều là những sai lầm tai hại thường thấy trong những cuộc thi mà kết quả lựa chọn chỉ dựa vào số lượng tin nhắn bình chọn.
Tất nhiên, khi kiểm định một giả thiết. Ta cố gắng hạn chế các sai lầm, tức là cần giảm thiểu tối đa xác suất phạm cả hai sai lầm. Tuy nhiên, đây là điều trong thực tế không thể làm được vì nếu ta muốn giảm sai lầm loại I thì sẽ làm tăng xác suất sai lầm loại II và ngược lại.
Có thể tóm tắt những quyết định xác suất dựa trên giả thuyết H0 như sau:

Còn tiếp…