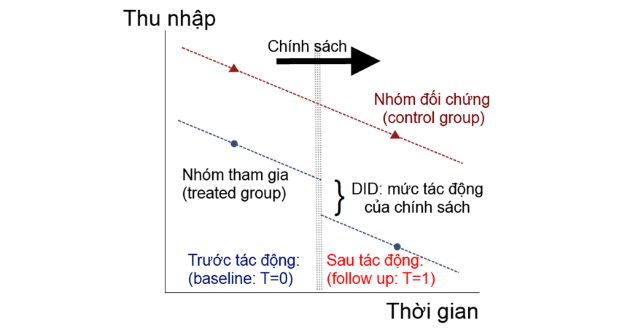
1. Giới thiệu phương pháp sai biệt képNội dung chính1. Giới thiệu phương pháp sai biệt kép2. Cách thực hiện DID3. Minh họa thực hiện DID Phương pháp khác biệt trong sự khác biệt (Difference in Differences) hay còn gọi là phương pháp sai biệt kép (DID) [World bank, 2010][1] ngày càng được sử dụng rộng rãi trong các nghiên cứu phân tích hiệu quả tác động của chính sách. Về cơ bản, phương pháp sai biệt kép so sánh các nhóm tác động và đối chứng dựa trên những khác biệt trong kết quả ở từng thời kỳ quan sát. Có nghĩa là, nếu có hai thời …