Phân biệt độ lệch chuẩn với sai số chuẩn

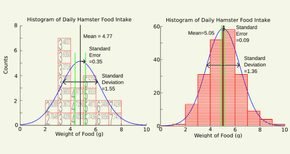
Nếu chúng ta chọn mẫu N lần, mỗi lần với n đối tượng thì chúng ta sẽ có N số trung bình. Độ lệch chuẩn của N số trung bình này chính là sai số chuẩn. Lưu ý, N ở đây là hàng triệu hay tỉ lần. Do đó, sai số chuẩn phản ảnh độ dao động hay biến thiên của các số trung bình mẫu (sample averages).

Tuy nhiên, không có cái gọi là “standard error of the mean”, mà chỉ có “standard deviation of the means”. Chữ means có “s” là số nhiều vì tính từ nhiều số trung bình. Thay vì gọi dài dòng là standard deviation of the means, người ta gọi ngắn gọn bằng một thuật ngữ mới: standard error.

2. Ý nghĩa của độ lệch chuẩn (SD) và sai số chuẩn (SE)

Gọi thông số trung bình của một quần thể là \(\mu \) (chúng ta không biết giá trị thật của \(\mu \)). Chúng ta có thể ước lượng gián tiếp \(\mu \) qua số trung bình của mẫu là \({\bar x}\) và độ lệch chuẩn của mẫu là s. Theo lí thuyết xác suất của phân phối chuẩn (dựa theo độ lệch chuẩn – SD), chúng ta có thể phát biểu rằng:

• 68% quan sát trong tổng thể đó có giá trị từ \({\bar x}\) ─ s đến \({\bar x}\) + s;
• 95% quan sát trong tổng thể đó có giá trị từ \({\bar x}\) ─ 1.96*s đến \({\bar x}\) + 1.96*s ;
• 99% quan sát trong tổng thể đó có giá trị từ \({\bar x}\) ─ 3*s đến \({\bar x}\) + 3*s.

Nếu gọi theo sai số chuẩn – SE, chúng ta có thể phát biểu rằng:

• 68% số trung bình từ mẫu có giá trị từ \({\bar x}\) ─ SE đến \({\bar x}\) + SE;
• 95% số trung bình từ mẫu có giá trị từ \({\bar x}\) ─ 1.96*SE đến \({\bar x}\) + 1.96*SE ;
• 99% số trung bình từ mẫu có giá trị từ \({\bar x}\) ─ 3*SE đến \({\bar x}\) + 3*SE.

Bài viết này được tổng hợp từ bài viết “Độ lệch chuẩn hay sai số chuẩn?” của Nguyễn Văn Tuấn trong chuyên đề Lâm sàng thống kê tại: ykhoa.net