Phân biệt độ lệch chuẩn với sai số chuẩn
Trong các tạp chí khoa học, chúng ta thường thấy những kí hiệu dạng x ± y, trong đó x là số trung bình, còn y thì có khi là độ lệch chuẩn (standard deviation – SD), đôi khi là sai số chuẩn (standard error – SE) hoặc SEM (standard error of the mean). Cách trình bày này thông dụng đến nỗi một số chuyên gia và các ban biên tập phải lên tiếng khuyến cáo (đưa ra quy ước chung). Theo đó:
- Nếu biến tuân theo luật phân phối chuẩn các nhà nghiên cứu nên theo cách trình bày số trung bình và kèm độ lệch chuẩn (không phải sai số chuẩn;
- Ngược lại, nếu biến không tuân theo luật phân phối chuẩn, nên trình bày số trung vị và số ở vị trí 25% và 75% (tức là interquartile range).

Để hiểu qui ước này, chúng ta cần phải tìm hiểu ý nghĩa của độ lệch chuẩn và sai số chuẩn. Đây là điều cần thiết, bởi hầu hết sách giáo khoa thống kê đều không giải rõ những khác biệt về ý nghĩa của hai chỉ số thống kê này.
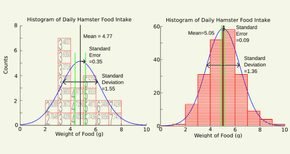
1. Sai số chuẩn – Standard error
Công thức tính sai số chuẩn (kí hiệu bằng SE – viết tắt từ standard error) rất đơn giản: lấy độ lệch chuẩn chia cho căn số bậc hai của số cỡ mẫu (n), \(SE = \frac{s}{{\sqrt n }}\)
Nguyên lí và mục đích đằng sau của thống kê học là ước tính những thông số của một quần thể (population). Trong thực tế chúng ta không biết các thông số này, mà chỉ dựa vào những ước tính từ một hay nhiều mẫu để suy luận cho giá trị của quần thể mà các mẫu được chọn. Chẳng hạn như chúng ta không biết chiều cao của người Việt là bao nhiêu (bởi vì đâu có ai đo lường chiều cao của gần 90 triệu dân); chúng ta phải chọn một mẫu gồm n đối tượng để tính trị số trung bình của mẫu này, và dùng trị số trung bình của mẫu để suy luận cho toàn dân số.

Nhưng chọn mẫu phải ngẫu nhiên thì mới mang tính đại diện cao. Cứ mỗi lần chọn mẫu, chúng ta có một nhóm đối tượng khác. Và, cứ mỗi mẫu, chúng ta có một số trung bình mới. Câu hỏi đặt ra là: nếu chọn mẫu nhiều lần (“nhiều” ở đây có nghĩa là hàng triệu hay tỉ lần) thì các số trung bình này dao động cỡ nào.