
Dạng hàm log – log
– Dạng hàm: \(lnY = {\beta _1} + {\beta _2}lnX\)
– Đồ thị:

– Tác động biên: \(m = {\beta _2}\frac{Y}{X}\)
– Độ co dãn: \(\varepsilon = {\beta _2}\)
Đối với dạng hàm này, tham số độ dốc chính là độ co dãn.
Để ước lượng OLS dạng hàm này chúng ta phải biến đổi dữ liệu của Y và X sang dạng logarit rồi ước lượng OLS logY theo logX.
3.Dạng hàm Lin – Log
– Dạng hàm: \(Y = {\beta _1} + {\beta _2}lnX\)
– Đồ thị:
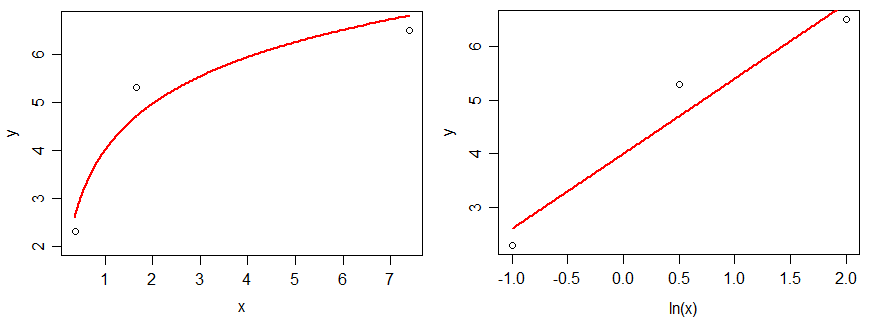
– Tác động biên: \(m = \frac{{{\beta _2}}}{X}\)
– Độ co dãn: \(\varepsilon = \frac{{{\beta _2}}}{{\bar Y}}\)
Khi tính toán kết quả của tác động biên và độ co dãn, X và Y được tính ở giá trị trung bình của mẫu. Xem X và Y là những hàng số, thì sai số chuẩn chính là căn bậc hai của phương sai. Cụ thể:
\(Var(\hat m) = {\left( {\frac{1}{{\bar X}}} \right)^2}Var({{\hat \beta }_2})\begin{array}{ccccccccccccccc}{}&{Var(\hat \varepsilon ) = {{\left( {\frac{1}{{\bar Y}}} \right)}^2}Var({{\hat \beta }_2})}\end{array}\)
Để ước lượng dạng hàm này, đầu tiên cần chuyển dạng dữ liệu của X sang dạng logarit. Sau đó hồi quy Y theo log của X.
4.Dạng hàm Log – Lin
– Dạng hàm: \(lnY = {\beta _1} + {\beta _2}X\)
– Đồ thị:
 – Tác động biên: \(m = {\beta _2}\bar Y\)
– Tác động biên: \(m = {\beta _2}\bar Y\)
– Độ co dãn: \(\varepsilon = {\beta _2}\bar X\)
Đối với dạng hàm này, tham số độ dốc \({\beta _2}\) có hiệu quả giải thích hữu ích. Khi X thay đổi 1 đơn vị, Y sẽ thay đổi xấp xỉ \({\beta _2}\)*100 phần trăm. Khi tính toán kết quả của tác động biên và độ co dãn, Y và X được tính ở mức giá trị trung bình của mẫu.
Kết quả sai số chuẩn của tác động biên và độ co dãn là căn bậc hai của phương sai, được tính theo các biểu thức sau:
\(Var(\hat m) = {\left( {\bar Y} \right)^2}Var({{\hat \beta }_2})\begin{array}{ccccccccccccccc}{}&{Var(\hat \varepsilon ) = {{\left( {\bar X} \right)}^2}Var({{\hat \beta }_2})}\end{array}\)
Để ước lượng dạng hàm này, đầu tiên chuyển dữ liệu của Y sang dạng Log của Y. Sau đó hồi quy log của Y theo X.