KTL nâng cao
Khắc phục phương sai thay đổi
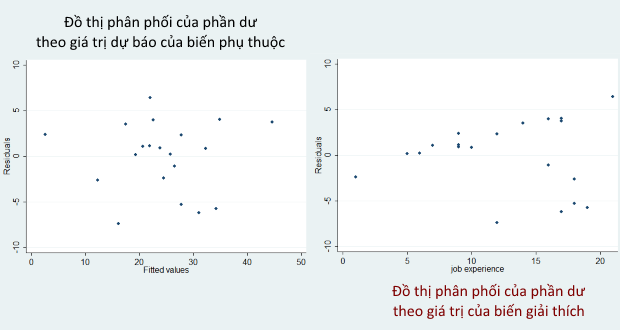
Các vấn đề về phương sai thay đổi và sự tự tương quan của phần dư trong mô hình hồi quy OLS tuy không làm thiên chệch kết quả ước lượng của hệ số nhưng sẽ làm kết quả ước lượng không hiệu quả, nhất là các sai số chuẩn ước lượng của hệ số không còn là bé nhất. Các phương pháp kiểm tra phương sai thay đổi thường được sử dụng là vẽ đồ thị phân phối phần dư theo biến giải thích hoặc biến phụ thuộc, sử dụng kiểm định Breusch-Pagan, kiểm định White tổng quát, kiểm định Goldfeldt-Quant; từ đó khắc phục bằng các …