Hồi quy Probit – STATA

2.

Giải thích kết quả hồi quy probit

• Trong bảng kết quả trên, chúng ta thấy kết quả hội tụ sau 4 lần lặp ở giá trị log likelihood bằng -229.20658. Giá trị log likelihood có thể được sử dụng để so sánh các mô hình với nhau. Sự chênh lệch giữa giá trị log likelihood trong mô hình probit vs mô hình logit không quá lớn (log likelihood hội tụ ở mô hình logit tương ứng là -229.25875).
• Ở dòng trên cùng của kết quả, chúng ta thấy cả 400 quan sát trong tập dữ liệu đều được sử dụng trong phân tích. Điều này bởi vì tập dữ liệu hiện sử dụng không có giá trị missing. Các giá trị missing sẽ được loại bỏ khỏi phân tích.
• LR chi2 (5) cho biết giá trị của thống kê chi bình phương (5 bậc tự do) bằng 41.56 với mức ý nghĩa p-value bằng 0.0001. Thống kê Chi2 này sẽ kiểm tra hiệu quả của mô hình probit so với mô hình không (không có biến giải thích nào), hay nói cách khác, Chi2 kiểm tra giả thuyết cho rằng hệ số ước lượng của 5 biến giải thích trong mô hình probit đều bằng 0. Với mức ý nghĩa p-value bằng 0.0001 cho thấy, mô hình probit là phù hợp.
• Tương tự như OLS, bảng hệ số cũng bao gồm thông tin về các hệ số ước lượng, sai số chuẩn, mức ý nghĩa, khoảng tin cậy… nhưng lưu ý, ở cột thống kê. Kiểm định hệ số trong hồi quy probit sử dụng thống kê z thay vì thống kê t như ở OLS. Kết quả cho thấy, cả gre, gpa và 3 biến giả của biến thứ tự rank đều có ý nghĩa thống kê ở mức 5%.
• Cách giải thích các hệ số của hồi quy probit tương tự như hồi quy logit. Các hệ số trong hồi quy probit cho biết sự thay đổi trong chỉ số logit (log của odds trong hồi quy logit) hoặc chỉ số probit (chỉ số logit trong hồi hồi quy logit) theo sự thay đổi 1 đơn vị của biến giải thích. Cụ thể, nếu giá trị của biến gre tăng thêm 1 đơn vị thì chỉ số probit sẽ tăng thêm 0.001; hoặc sự tăng thêm 1 đơn vị của biến gpa sẽ làm tăng thêm 0.478 ở chỉ số probit.
• Cách giải thích của các biến giả i.rank có khác đôi chút so với các biến liên tục. Ở đây, hệ số của các biến giả 2.rank 3.rank 4.rank là so sánh với giá trị tham chiếu 1.rank. Cụ thể, những học sinh học ở trường THCS được xếp hạng thứ 2 (rank=2)thì sẽ có chỉ số probit thấp hơn so với học sinh các trường THCS được xếp hạng cao nhất (rank=1) là 0.415.

Để hiểu rõ hơn về mô hình, chúng ta tìm hiểu về xác suất được dự báo. Xác suất được dự báo của mô hình được tính bằng câu lệnh margins. Phần tùy chọn phía sau lệnh margins là chỉ rõ giá trị cụ thể của mức xác suất dự báo. Chẳng hạn, chúng ta muốn biết xác suất được xét tuyển vào trường PTTH theo các mức xếp hạng của trường THCS tại giá trị trung bình của các biến gre, gpa như sau:

margins rank, atmeans

Trong bảng kết quả trên, chúng ta thấy rằng mức xác suất để được xét tuyển vào trường PTTH là 0.52 cho học sinh trường THCS được xếp hạng cao nhất (rank = 1) và 0.19 cho học sinh trường THCS được xếp hạng thấp nhất (rank = 4) tại giá trị trung bình của 2 biến gre và gpa.

Bây giờ, chúng ta muốn lập bảng giá trị xác suất được dự đoán tại một khoảng giá trị cụ thể của một biến. Chẳng hạn mức giá trị xác suất được dự báo ứng với sự thay đổi của biến gre từ 200 đến 800 với bước nhảy là 100.

Bởi vì chúng ta không chỉ rõ giá trị của các biến còn lại (atmeans hoặc used at (…)) do vậy, giá trị trong bảng là giá mức xác suất dự báo trung bình dựa trên các giá trị của các biến giải thích còn lại trong mẫu. Chẳng hạn, để tính toán giá trị xác suất được dự đoán trung bình khi gre = 200, thì mức xác suất được dự báo này sẽ được tính cho tất cả các quan sát ứng với mức gre = 200.

margins, at(gre=(200(100)800)) vsquish

Trong bảng trên, chúng ta có thể thấy giá trị trung bình của xác suất được báo được xét tuyển là 0.16 nếu một học sinh có điểm GRE bằng 200 và tăng lên 0.42 nếu học sinh đó có điểm GRE là 800.

3.

Đồ thị minh họa xác suất dự đoán của hồi quy probit

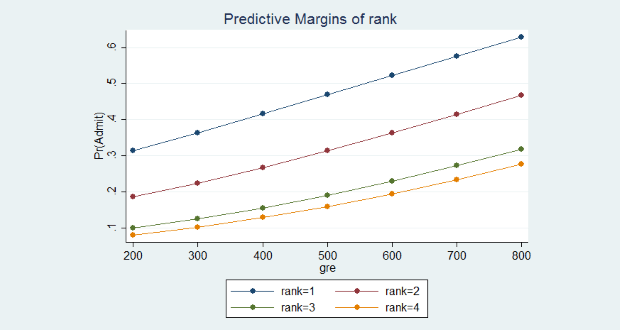
Đồ thị xác suất được dự đoán trên theo các mức được xếp hạng của trường THCS được thể hiện như sau:

Với đồ thị này, tương ứng với mỗi mức giá trị GRE thì xác suất được xét tuyển vào PTTH của những học sinh của trường THCS được xếp hạng 1 luôn cao hơn tương ứng với học sinh trường THCS nhóm 2, 3 và 4. Chẳng hạn, cùng một điểm số GRE là 200, khả năng được xét tuyển ở nhóm trường hạng 4 chưa đến 10% trong khi đó khả năng này ở những học sinh nhóm trường hạng 1 là trên 30%.

Điều này cũng hoàn toàn tương tự ở các mức xác suất được dự đoán theo các mức được xếp hạng của trường THCS ở các mốc giá trị của điểm trung bình GPA.

Ngoài ra, để kiểm tra mức độ phù hợp của mô hình, chúng ta có thể sử dụng lệnh fitstat. Lệnh fitstat sẽ tổng hợp các thông số về độ phù hợp của mô hình. Chúng ta có thể sử dụng kết quả này để lựa chọn một mô hình phù hợp. Các bạn sử dụng lệnh findit fitstat để thêm lệnh vào chương trình (nếu chưa có).

fitstat

2. Với kết quả hồi quy probit so với hồi quy logit được thể hiện ở bảng bên dưới, các bạn hãy cho nhận xét về mối quan hệ giữa các hệ số của 2 mô hình.

1. Long, J. Scott (1997). Regression Models for Categorical and Limited Dependent Variables. Thousand Oaks, CA: Sage Publications.