Hồi quy nhị thức âm – STATA

Hồi quy nhị thức âm (Negative Binomial Regression) được sử dụng để ước lượng các mô hình với dữ liệu của biến phụ thuộc có dạng đếm (counts) và phân tán rộng. Dữ liệu được xem là phân tán rộng khi biến có sai số chuẩn vượt quá giá trị trung bình của biến. Đây là dạng tổng quát của hồi quy Poisson.

Ví dụ: Chúng ta muốn dự báo thái độ chuyên cần của các sinh viên trong các ngành ở 2 trường đại học. Biến giải thích là số ngày nghỉ học, chuyên ngành học và điểm môn toán (được chuẩn hóa).

Phần minh họa sử dụng dữ liệu thực hành là nbreg.dta

use https://www.vietlod.com/data/nbreg.dta, clear

Bộ dữ liệu bao gồm 3 biến daysabs math và prog với 314 quan sát. Thông tin cụ thể của các biến như sau:

• Biến prog là ngành học, có dạng danh mục với 3 giá trị: 1 (tổng quát), 2 (học thuật) và 3 (hướng nghiệp).
• Biến daysabs là số ngày nghỉ học.
• Biến math là điểm thi toán, là 1 biến liên tục.

summarize daysabs math

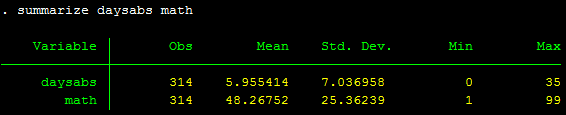
Nhận xét: biến phụ thuộc có giá trị trung bình thấp hơn độ lệch chuẩn

histogram daysabs, discrete freq scheme(s1mono)

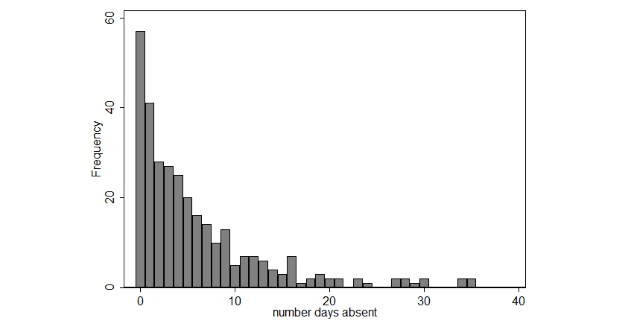
Kết quả thống kê của số ngày nghỉ ở từng chuyên ngành được thể hiện như hình bên dưới. Theo đó, biến prog là biến giải thích tốt cho biến kết quả, bởi giá trị trung bình của nó thay đổi nhiều ở các chuyên ngành.

tabstat daysabs, by(prog) stats(mean v n)

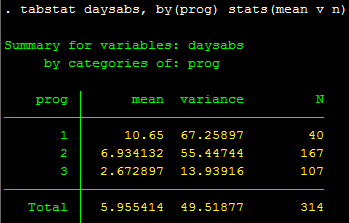
Lựa chọn phương pháp phân tích

• Hồi quy poisson
• Zero-inflated regression model – được sử dụng khi dữ liệu của biến phụ thuộc tập trung rất gần 0. Mô hình Zero-inflated sẽ ước lượng đồng thời 2 biểu thức theo hồi quy logit (dữ liệu tập trung gần 0) và hồi quy poisson (dữ liệu đếm)
• Hồi quy OLS – Các biến đếm sẽ được chuyển sang dạng logarit và được đưa vào sử dụng trong phân tích hồi quy tuyến tính OLS. Vì vậy, xảy ra hiện tượng mất mát thông tin, đồng thời phát sinh lỗi trong quá trình logarit hóa (các quan sát có giá trị đếm bằng 0).

Thực hiện hồi quy nhị thức âm

Phần trình bày bên dưới sẽ minh họa cách hồi quy nhị thức âm trên STATA.

Hồi quy nhị thức âm trên Stata được thự hiện bằng lệnh nbreg. Tiền tố i. để xác định biến danh mục cho biến prog đứng sau.

nbreg daysabs math i.prog

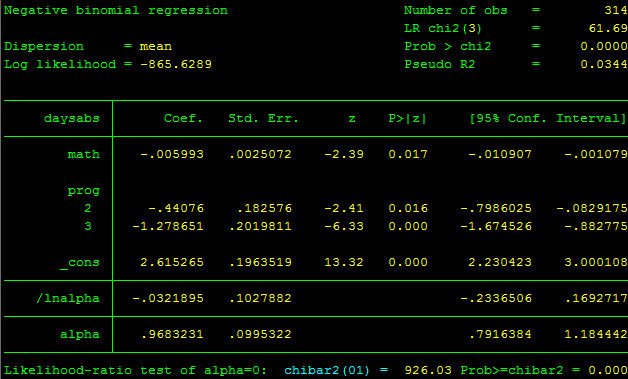
• Phần kết quả bắt đầu với kết quả các quá trình lặp. Chúng ta thấy rằng mô hình được bắt đầu ước lượng bằng hồi quy poisson, sau đó là mô hình không (chỉ bao gồm hệ số cắt) và cuối cùng là mô hình đầy đủ. Giá trị tuyệt đối của log likelihood giảm dần sau mỗi quá trình lặp. Giá trị log likelihood của mô hình cuối cùng là -865.6289, và giá trị này được sử dụng để so sánh lựa chọn mô hình.
• Kế tiếp là bảng tổng hợp kết quả về độ phù hợp của mô hình. Thống kê Ward Chi2 với 3 bậc tự do 61.69 cho thấy mô hình đầy đủ với 3 biến giải thích phù hợp hơn so với mô hình không. Kết quả này có ý nghĩa thống kê 1%. Giá trị pseudo-R2 bằng 0.034 cũng được trình bày ở đây.
• Bên dưới bảng thông tin về độ phù hợp của mô hình là các thông tin về hệ số hồi quy Poisson như hệ số ước lượng, sai số chuẩn, chỉ số z, mức ý nghĩa và khoảng tin cậy 95% của hệ số. Kết quả cho thấy các biến đều có ý nghĩa thống kê 5%.
• Giá trị hệ số ước lượng của biến math bằng -0.006 cho biết cứ tăng thêm 1 đơn vị trong giá trị của biến math sẽ làm giảm giá trị kì vọng log của biến daysabs 0.006 đơn vị. Hoặc hệ số của biến 2.prog bằng 0.44 có ý nghĩa rằng so với nhóm prog=1 thì giá trị kì vọng log của daysabs thấp hơn 0.44 lần. Điều này cũng tương tự ở nhóm prog = 3.

Để xác định xem biến bản thân biến prog có ý nghĩa thống kê hay không, chúng ta có thể sử dụng lệnh test như sau:

test 2.prog 3.prog
( 1) [daysabs]2.prog = 0
( 2) [daysabs]3.prog = 0

chi2( 2) = 49.21
Prob > chi2 = 0.0000

Ngoài ra, Stata sử dụng ước lượng hợp lí cực đại để ước lượng giá trị logarit của anpha và từ đó tính anpha như trong bảng kết quả trên. Giá trị anpha bị ràng buộc bằng 0 trong hồi quy poisson. Điều này nghĩa là anpha luôn lớn hơn 0 và lệnh nbreg chấp nhận dữ liệu phân tán (phương sai lớn hơn giá trị trung bình).

Bên dưới bảng hệ số, chúng ta sẽ thấy kết quả kiểm định LR cho rằng anpha bằng 0 (so sánh với mô hình hồi quy Poisson) . Trong ví dụ này với giá trị Chi2 (1 bậc tự do) bằng 926.03 cho thấy anpha khác 0 luôn có ý nghĩa thống kê dưới 1% và mô hình hồi quy nhị thức âm là mô hình phù hợp hơn (hồi quy Poisson).

Đôi khi, chúng ta sử dụng dạng tỉ lệ thay vì dạng log của các hệ số để giải thích. Đây chính là dạng mũ hóa các hệ số ước lượng từ phương trình:

log(daysabs) = Intercept + b1(prog=2) + b2(prog=3) + b3math.

Mũ hóa hai vế:

daysabs = exp(Intercept + b1(prog=2) + b2(prog=3)+ b3math) = exp(Intercept) * exp(b1(prog=2)) * exp(b2(prog=3)) * exp(b3math)

Bằng cách thêm tùy chọn irr phía sau câu lệnh nbreg như sau:

nbreg, irr

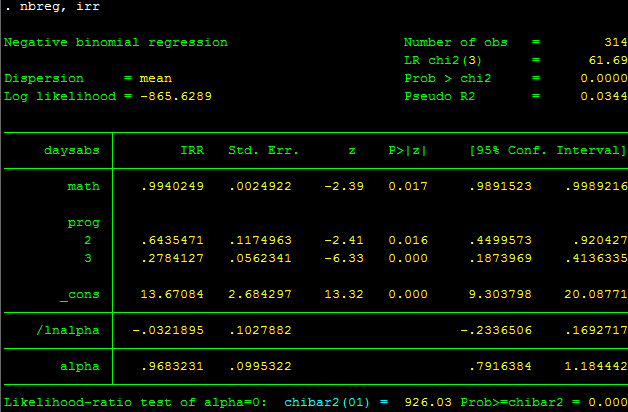
Kết quả trên cho thấy tỉ lệ IRR cho biến 2.prog và 3.prog lần lượt bằng 0.64 và 0.28 lần so với nhóm tham chiếu (prog=1). Đối với biến math, thì một sự gia tăng 1 đơn vị của biến này sẽ làm giảm 1% trong IRR của biến daysabs.

Để dễ hiểu và giải thích mô hình, chúng ta sử dụng lệnh margins để tính toán các giá trị đếm dự đoán của biến daysabs tại các mức giá trị của biến prog, trong khi giữ nguyên giá trị các biến còn lại tại giá trị trung bình của biến.

margins prog, atmeans

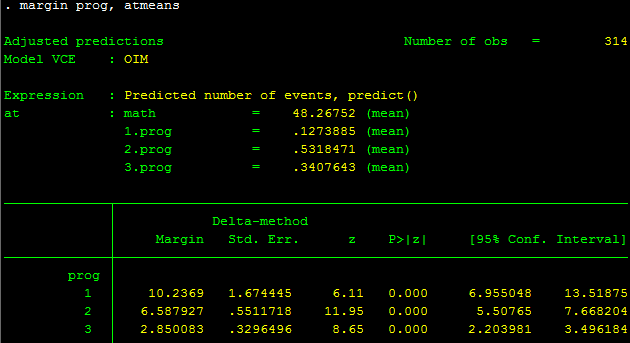
Trong bảng kết quả trên, chúng ta thấy rằng số ngày nghỉ ở nhóm prog=1 là 10.24; prog=2 là 6.59 và prog=3 là 2.85 (tại giá trị trung bình của biến math)

Hoặc chúng ta cũng có thể dự đoán số ngày nghỉ theo sự thay đổi điểm math (thay đổi từ 0 đến 100 với bước nhảy là 20).

margins, at(math=(0(20)100)) vsquish

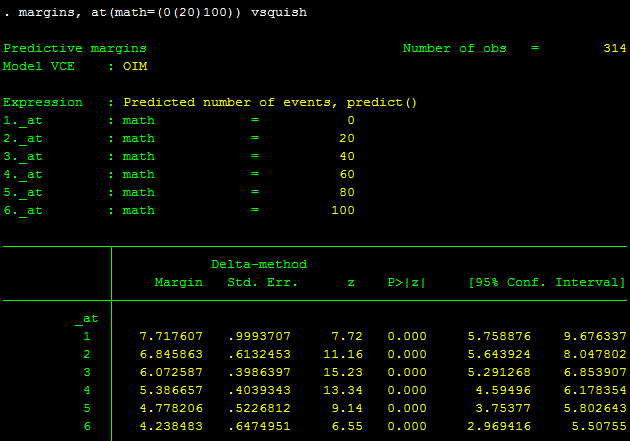
Bảng kết quả trên cho thấy rằng tại giá trị biến math bằng 0 thì giá trị dự đoán của biến daysabs là 7.72 và khi giá trị của math bằng 100 thì giá trị dự đoán của daysabs là 4.24.

Thông tin chi tiết về mô hình được tổng hợp trong kết quả của lệnh fitstat như sau:

fitstat

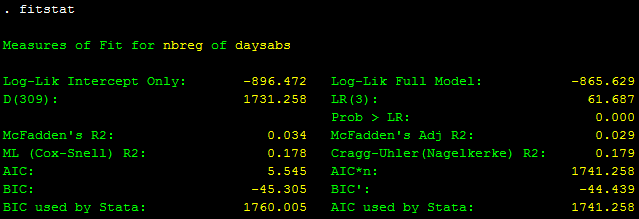
Các bạn có thể minh họa giá trị dự đoán của biến daysabs bằng đồ thị như sau:

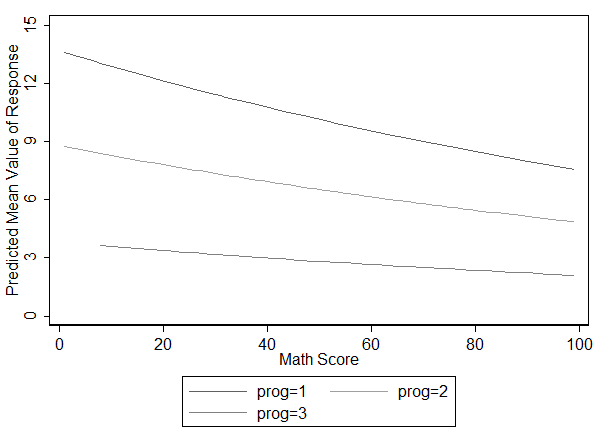
Kết quả cho thấy, chuyên ngành tổng quát (prog=1) được dự đoán có số giải thưởng nhiều nhất, đặc biệt trong trường hợp sinh viên có điểm toán thấp. Số giải thưởng được dự báo ít nhất trong ngành hướng nghiệp (prog=3)