Diễn giải chi tiết kết quả hồi quy logit
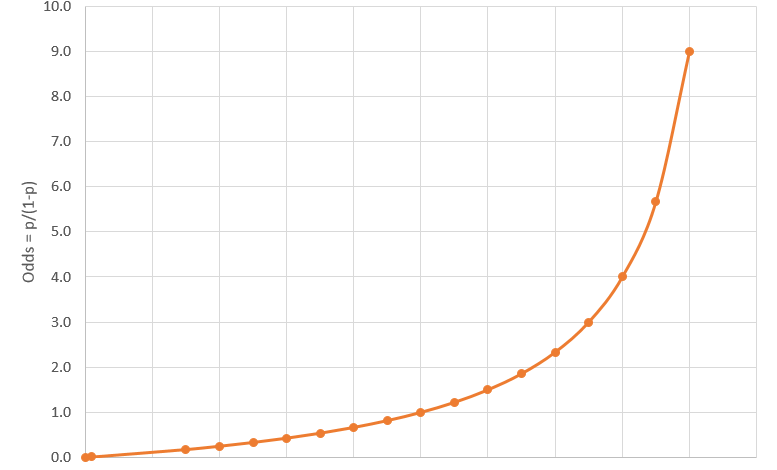
3. Hồi quy logit đơn giản với biến giải thích dạng liên tục
Trong trường hợp hồi quy khả năng được vinh danh của một học sinh theo một biến liên tục, chẳng hạn điểm số môn toán (math) thì kết quả mô hình được giải thích khác đôi chút. Trong trường hợp này, hệ số cắt là logit của một học sinh có điểm toán học bằng 0 được vinh danh . Nói cách khác, giá trị odds của một học sinh trong lớp được vinh danh khi điểm số môn toán bằng 0 là exp(-9,793942) = 0.00005579. Giá trị odds này là rất thấp, tuy nhiên, nếu chúng ta nhìn vào sự phân bố điểm của môn toán thì thấy rằng không có một học sinh nào trong các mẫu có điểm điểm thấp hơn 30. Tất cả các điểm thi trong tập dữ liệu đã được chuẩn hóa xung quanh giá trị trung bình của 50 và độ lệch chuẩn là 10. Vì vậy, hệ số chặn trong mô hình này tương ứng với logit được tặng bằng khen khi điểm toán được giả định là bằng 0.
Các hệ số ước lượng của môn toán được giải thích như thế nào? Các hệ số ước lượng và hệ số cắt trong phương trình sau logit(p) = β0 + β1*math
. logit honor math Iteration 0: log likelihood = -111.35502 Iteration 1: log likelihood = -85.690395 Iteration 2: log likelihood = -83.554079 Iteration 3: log likelihood = -83.536627 Iteration 4: log likelihood = -83.536619 Iteration 5: log likelihood = -83.536619 Logistic regression Number of obs = 200 LR chi2(1) = 55.64 Prob > chi2 = 0.0000 Log likelihood = -83.536619 Pseudo R2 = 0.2498 ------------------------------------------------------------------------------ honor | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- math | .1563404 .0256096 6.10 0.000 .1061465 .2065342 _cons | -9.793942 1.48175 -6.61 0.000 -12.69812 -6.889765 ------------------------------------------------------------------------------
logit(p) = log(p/(1-p)) = – 9.793942 + .1563404*math
- Khi math = 54 thì logit của việc được vinh danh là log(p/(1-p))(math=54) = – 9.793942 + 0.1563404 *54.
- Khi math tăng thêm 1 đơn vị (55 = 54 + 1) thì là log(p/(1-p))(math=55) = – 9.793942 + 0.1563404 *55.
- Ứng với việc gia tăng 1 đơn vị của math thì logit của việc được vinh danh sẽ thay đổi một lượng log(p/(1-p))(math=55) – log(p/1-p))(math = 54) = 0.1563404.
Vì vậy, chúng ta có thể nói rằng hệ số ước lượng của math chính là sự khác biệt trong logit khi math thay đổi một đơn vị. Nói cách khác, ứng với một sự gia tăng một đơn vị trong số điểm môn toán, kì vọng sẽ thay đổi một lượng 0.1563404 trong logit.
Chúng ta cũng có thể biểu diễn dạng logit thành dạng tỉ lệ odds thông qua câu lệnh logistic hoặc logit với tùy chọn or. Kết quả tỉ lệ odds trong mô hình khi đó sẽ là:
. logit honor math, or Iteration 0: log likelihood = -111.35502 Iteration 1: log likelihood = -85.690395 Iteration 2: log likelihood = -83.554079 Iteration 3: log likelihood = -83.536627 Iteration 4: log likelihood = -83.536619 Iteration 5: log likelihood = -83.536619 Logistic regression Number of obs = 200 LR chi2(1) = 55.64 Prob > chi2 = 0.0000 Log likelihood = -83.536619 Pseudo R2 = 0.2498 ------------------------------------------------------------------------------ honor | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- math | 1.169224 .0299433 6.10 0.000 1.111985 1.22941 _cons | .0000558 .0000827 -6.61 0.000 3.06e-06 .0010182 ------------------------------------------------------------------------------
Hoặc được tính bằng tay là
= exp[logit(p)(math=55) – logit(p)(math = 54)]
= exp(logit(p)(math=55)) / exp(logit(p)(math = 54))
= odds(math=55)/odds(math=54)
= exp(0.1563404) = 1.1692241
Điều này có nghĩa một sự gia tăng một đơn vị trong điểm môn toán được mong đợi sẽ làm tăng khoảng 17% trong tỷ lệ odds của việc được vinh danh trong lớp học. Mức tăng 17% này không phụ thuộc vào một giá trị cụ thể của điểm số toán, nó luôn ứng với bất kì sự gia tăng một điểm trong môn toán.