Bảng tra phân phối Student – t

Phân phối Student là công cụ thống kê quan trọng trong kiểm định giả thuyết, đặc biệt khi kích thước mẫu nhỏ. Việc nắm vững định lý, tính chất và cách tra bảng giúp cải thiện độ chính xác trong phân tích dữ liệu. Bài viết giải thích định nghĩa, tính chất và ứng dụng thực tế của phân phối này, kèm theo ví dụ cụ thể và bảng tra cứu.

1. Giới thiệu về Phân Phối Student

Phân phối Student (hay còn gọi là phân phối t) được sử dụng phổ biến trong thống kê, đặc biệt trong các kiểm định giả thuyết về giá trị trung bình khi kích thước mẫu nhỏ. Phân phối này thường kết hợp với các phân phối khác như chi bình phương và F để kiểm định hiệu quả mô hình thống kê.

2. Định lý Phân Phối Student

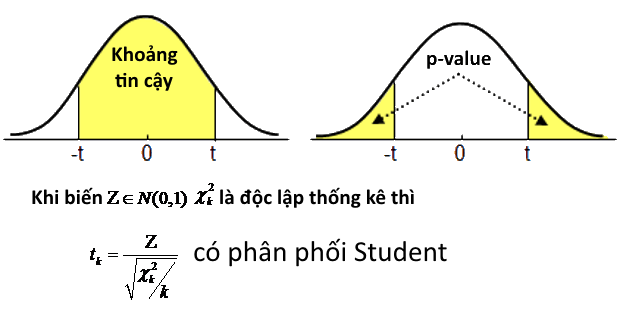
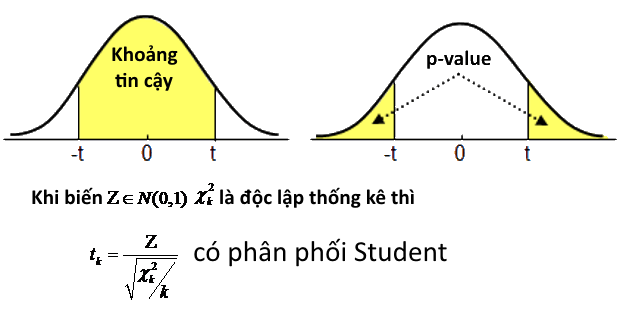
Nếu $Z \sim N(0,1)$ và $\chi_k^2$ là độc lập thống kê, thì:

$$t_k = \frac{Z}{\sqrt{\chi_k^2 / k}}$$

tuân theo phân phối Student với $k$ bậc tự do.

3. Tính chất Phân Phối Student

• Đối xứng quanh 0, tương tự như phân phối chuẩn hóa.
• Khi bậc tự do lớn ($k > 30$), phân phối Student tiệm cận phân phối chuẩn hóa.
• Trong thực hành, khi $k > 30$, ta có thể coi phân phối Student là phân phối chuẩn hóa $N(0, k/(k-2))$.

4. Ví dụ Tra Bảng Phân Phối Student

Bài toán: Mẫu kích thước $n = 32$ có trung bình mẫu $\bar{x} = 128.5$ và sai số chuẩn $SE = 6.2$. Hãy tính khoảng tin cậy 99% cho giá trị trung bình.

• Bậc tự do: $DF = n-1 = 31$
• Giá trị $t$: $t = 2.744$

Khoảng tin cậy:

$$(128.5 – 2.744 \times 6.2; 128.5 + 2.744 \times 6.2) = (111.5; 145.5)$$

5. Bảng Tra Phân Phối Student

Xem thêm:

• Bảng tra phân phối F
• Bảng tra phân phối Chi bình phương