Sơ lược về hồi quy Logit
Kết quả ước lượng của một biến phụ thuộc dạng nhị phân trong các hồi quy logit có được dựa trên giả định rằng việc chuyển đổi logit của biến phụ thuộc có một mối quan hệ tuyến tính với các biến giải thích. Điều này làm cho việc giải thích của các hệ số hồi quy của mô hình khác đôi chút so với mô hình hồi quy OLS. Trong chuyên mục này, chúng tôi sẽ đi qua các khái niệm về tỷ số odds và cố gắng giải thích các kết quả hồi quy logit trong một vài ví dụ.
Xem thêm các bài viết:
- Diễn giải chi tiết kết quả hồi quy logit
- Chẩn đoán kết quả mô hình hồi quy logit
- Phát hiện các khuyết tật dữ liệu trong mô hình hồi quy logit
- Đọc và chẩn đoán kết quả mô hình hồi quy logit thứ tự
Từ xác suất đến odds và log của odds
Mọi thứ bắt đầu với khái niệm về xác suất. Giả sử, xác suất thành công của một sự kiện Manchester United vô địch Premier League mùa giải 2016 – 2017 là 0.2 thì xác suất thất bại của sự kiện này sẽ là 1 – 0.2 = 0.8. odds của sự kiện thành công được định nghĩa là tỷ lệ xác suất thành công trên xác suất thất bại của sự kiện. Trong ví dụ trên, odds của MU vô địch là 0.2 / 0.8 = 1/4. Điều đó nói lên rằng tỉ lệ odds của sự kiện là 1 trên 4 (tạm hiểu odds là tỉ lệ cược hay tỉ lệ thành công của sự kiện MU vô địch là đặt 1 ăn 4).
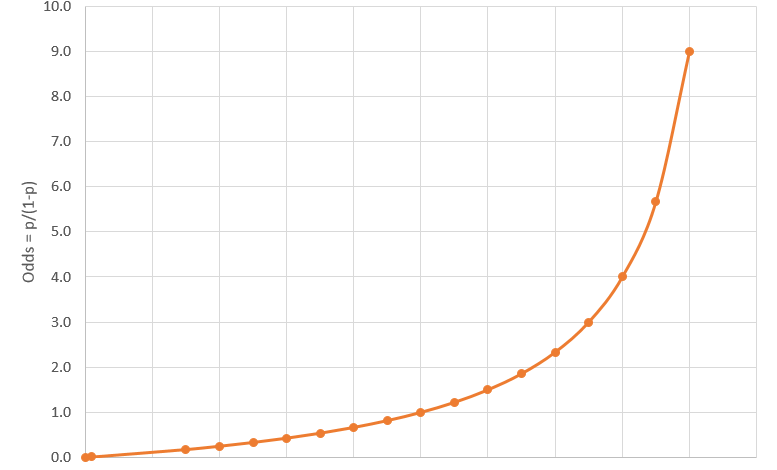
Việc chuyển đổi từ xác suất đến tỷ lệ cược là một biến đổi đơn điệu (monotonic transformation), nghĩa là odds của sự kiện tăng thì xác suất thành công của sự kiện đó cũng tăng và ngược lại. Giá trị xác suất dao động từ 0 đến 1 nhưng odds dao động từ 0 đến vô cực.
Biểu đồ về mối quan hệ giữa giá trị xác suất (p) và giá trị odds được thể hiện như sau:
