500 câu trắc nghiệm Kinh tế lượng – 8C

SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Use the computer display to solve the problem.
14) When testing for a difference between the means of a treatment group and a placebo group, the computer display below is obtained. Using a 0.04 significance level, is there sufficient evidence to support the claim that the treatment group (variable 1) comes from a population with a mean that is different from the mean for the placebo population? Explain.
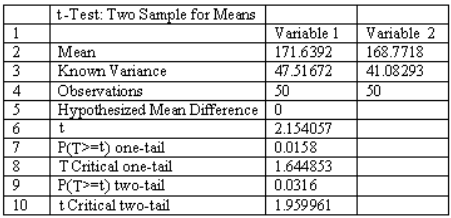
Yes, the P-value for a two-tail test is 0.0316, which is smaller than the significance level of 0.04. There is sufficient evidence to support the claim that the two population means are different.
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Assume that you want to test the claim that the paired sample data come from a population for which the mean difference is md = 0. Compute the value of the t test statistic.
15) The following table shows the weights of nine subjects before and after following a particular diet for two months. You wish to test the claim that the diet is effective in helping people lose weight. What is the value of the appropriate test statistic?
| Subject | A | B | C | D | E | F | G | H | I |
| Before | 168180157132202124 | 190 | 210 | 171 | |||||
| After | 162178145125171126 | 180 | 195 | 163 |
○ 9.468
○ 0.351
● 3.156
○ 1.052
Determine the decision criterion for rejecting the null hypothesis in the given hypothesis test; i.e., describe the values of the test statistic that would result in rejection of the null hypothesis.
16) We wish to compare the means of two populations using paired observations. Suppose that \(\bar d\) = 3.125, Sd = 2.911, and n = 8, and that you wish to test the following hypothesis at the 5 percent level of significance:
H0: \({\mu _d}\) = 0 against H1: \({\mu _d}\) > 0.
What decision rule would you use?
○ Reject H0 if test statistic is greater than -1.895 and less than 1.895.
● Reject H0 if test statistic is greater than 1.895.
○ Reject H0 if test statistic is less than 1.895.
○ Reject H0 if test statistic is greater than -1.895.
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
Use the traditional method of hypothesis testing to test the given claim about the means of two
populations. Assume that two dependent samples have been randomly selected from normally distributed populations.
17) A coach uses a new technique to train gymnasts. 7 gymnasts were randomly selected and their competition scores were recorded before and after the training. The results are shown below.
| Subject | A | B | C | D | E | F | G |
| Before | 9.49.7 | 9.6 | 9.5 | 9.7 | 9.6 | 9.7 | |
| After | 9.59.9 | 9.6 | 9.4 | 9.8 | 9.9 | 9.5 |
Using a 0.01 level of significance, test the claim that the training technique is effective in raising the gymnasts’ scores.
Test statistic t = -0.880. Critical value: t = -3.143.
Fail to reject H0: \({\mu _d}\ = 0. There is not sufficient evidence to support the claim that the technique is effective in raising the gymnasts’ scores.
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Construct a confidence interval for \({\mu _d}\), the mean of the differences d for the population of paired data. Assume that the population of paired differences is normally distributed.
18) A test of abstract reasoning is given to a random sample of students before and after they completed a formal logic course. The results are given below. Construct a 95% confidence interval for the mean difference between the before and after scores.
| Before | 74 | 83 | 75 | 88 | 84 | 63 | 93 | 84 | 91 | 77 |
| After | 73 | 77 | 70 | 77 | 74 | 67 | 95 | 83 | 84 | 75 |
○ 1.2 < \({\mu _d}\) < 5.7
○ 0.8 < \({\mu _d}\) < 6.6
● 0.2 < \({\mu _d}\) < 7.2
○ 1.0 < \({\mu _d}\) < 6.4
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
Test the indicated claim about the variances or standard deviations of two populations. Assume that the populations are normally distributed. Assume that the two samples are independent and that they have been randomly selected.
19) Test the claim that populations A and B have different variances. Use a significance level of 0.10.
| Sample A | Sample B |
| n = 28 | n = 41 |
| \({{\bar x}_1}\) = 19.2 | \({{\bar x}_2}\) = 23.7 |
| s = 4.56 | s = 5.66 |
H0: \(\sigma _1^2\) = \(\sigma _2^2\). H1: \(\sigma _1^2\) > \(\sigma _2^2\).
Test statistic: F = 1.541. Critical value: F = 1.836.
Fail to reject the null hypothesis. There is not sufficient evidence to support the claim that populations A and B have different variances.
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Solve the problem.
20) When performing a hypothesis test for the ratio of two population variances, the upper critical F value is denoted FR. The lower critical F value, FL, can be found as follows: interchange the degrees of freedom, and then take the reciprocal of the resulting F value found in table A-5. FR can be denoted \({F_{\alpha /2}}\) and FL can be denoted \({F_{1- \alpha /2}}\).
Find the critical values FL and FR for a two-tailed hypothesis test based on the following values:
n1 = 4, n2 = 8, \(\alpha \) = 0.05
○ 0.1211, 4.3541
○ 0.1703, 5.8898
● 0.0684, 5.8898
○ 0.1112, 5.0453