500 câu trắc nghiệm Kinh tế lượng – 11A

Use the Minitab display to test the indicated claim.
9) A manager records the production output of three employees who each work on three different machines for three different days. The sample results are given below and the Minitab results follow.
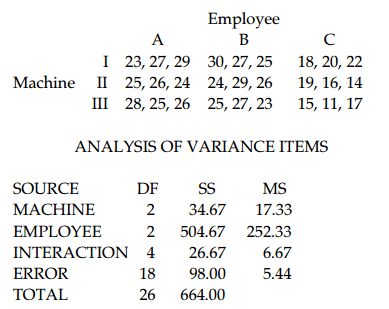
Using a 0.05 significance level, test the claim that the interaction between employee and machine has no effect on the number of items produced.
H0: There is no interaction effect.
H1: There is an interaction effect.
Test statistic: F = 1.2261. Critical value: F = 2.9277.
Fail to reject the null hypothesis. There does not appear to be an interaction effect.
10) A manager records the production output of three employees who each work on three different machines for three different days. The sample results are given below and the Minitab results follow.
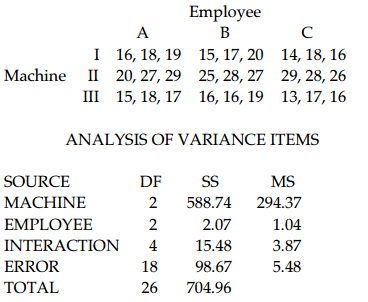
Assume that the number of items produced is not affected by an interaction between employee and machine. Using a 0.05 significance level, test the claim that the machine has no effect on the number of items produced.
H0: There is no machine effect.
H1: There is a machine effect.
Test statistic: F = 53.7172. Critical value: F = 3.5546.
Reject the null hypothesis. There does appear to be a machine effect.
11) A manager records the production output of three employees who each work on three different machines for three different days. The sample results are given below and the Minitab results follow.
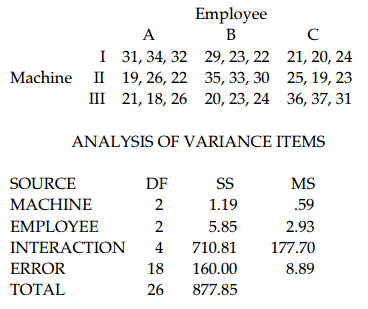
Assume that the number of items produced is not affected by an interaction between employee and machine. Using a 0.05 significance level, test the claim that the choice of employee has no effect on the number of items produced.
H0: There is no employee effect.
H1: There is an employee effect.
Test statistic: F = 0.3296. Critical value: F = 3.5546.
Fail to reject the null hypothesis. There does not appear to be an employee effect.
Use the data in the given table and the corresponding Minitab display to test the hypothesis.
12) The following table entries are the times in seconds for three different drivers racing on four different tracks. Assuming no effect from the interaction between driver and track, test the claim that the three drivers have the same mean time. Use a 0.05 significance level.
| Track 1 | Track 2 | Track 3 | Track 4 | |
| Driver 1 | 72 | 70 | 68 | 71 |
| Driver 2 | 74 | 71 | 66 | 72 |
| Driver 3 | 76 | 69 | 64 | 70 |
| Source | DF | SS | MS | F | p |
| Driver | 2 | 2 | 1 | 0.33 | 0.729 |
| Track | 3 | 98.25 | 32.75 | 10.92 | 0.00763 |
| Error | 6 | 18 | 3 | ||
| Total | 11 | 118.25 |
H0: There is no driver effect. H1: There is a driver effect. The P-value is 0.729, which is greater than 0.05. We fail to reject the null hypothesis; it appears that the driver does not affect the racing times
13) The following minitab display results from a study in which three different teachers taught calculus classes of five different sizes. The class average was recorded for each class. Assuming no effect from the interaction between teacher and class size, test the claim that the teacher has no effect on the class average. Use a 0.05 significance level.
| Source | DF | SS | MS | F | p |
| Teacher | 2 | 56.93 | 28.47 | 1.018 | 0.404 |
| Class Size | 4 | 672.67 | 168.17 | 6.013 | 0.016 |
| Error | 8 | 223.73 | 27.97 | ||
| Total | 14 | 953.33 |
H0: There is no teacher effect. H1: There is a teacher effect. The P-value is 0.404, which is greater than 0.05. We fail to reject the null hypothesis; it appears that the teacher does not affect the class average.
Provide an appropriate response.
14) The following results are from a statistics package in which all of the F values and P-values are given. Is there a significant effect from the interaction? Should you test to see if there is a significant effect due to either A or B? If the answer is yes, is there a significant effect due to either A or B?
ANOVA Table
| Source | DF | Sum squares | Mean square | F test | P-value |
| A | 2 | 415.87305 | 207.93652 | 1.88259 | .1637 |
| B | 3 | 2997.47186 | 999.15729 | 9.04603 | .0001 |
| Interaction | 6 | 707.26626 | 117.87771 | 1.06723 | .3958 |
| Error | 46 | 5080.81667 | 110.45254 | ||
| Total | 57 | 9201.42784 |
Since P = 0.3958 for the interaction, you fail to reject the null hypothesis that there is no effect due to the
interaction. Yes, it is appropriate to see if there is a significant effect due to either A or B. The P-value
for B is P = 0.0001, which rejects the null hypothesis that there is no effect due to B. The means for B are
not all the same.
15) The following data shows annual income, in thousands of dollars, categorized according to the two factors of gender and level of education. Assume that incomes are not affected by an interaction between gender and level of education, and test the null hypothesis that gender has no effect on income. Use a 0.05 significance level.
| Female | Male | |
| High school | 23, 27, 24, 26 | 25, 26, 22, 24 |
| College | 28, 36, 31, 33 | 35, 32, 39, 28 |
| Advanced degree | 41, 38, 43, 49 | 35, 50, 47, 44 |
H0: Gender has no effect on income. H1: Gender has an effect on income. The test statistic is F = 0.155591, and the corresponding P-value is 0.697883. Because the P-value is greater than 0.05, we fail to reject the null hypothesis that gender has no effect on income.
16) The following data contains task completion times, in minutes, categorized according to the gender of the machine operator and the machine used.
| Male | Female | |
| Machine 1 | 15, 17 | 16, 17 |
| Machine 2 | 14, 13 | 15, 13 |
| Machine 3 | 16, 18 | 17, 19 |
Assume that two-way ANOVA is used to analyze the data. How are the ANOVA results affected if 5 minutes is added to each completion time?
The ANOVA results are not affected by adding 5 minutes to each completion time.
The null hypothesis of no interaction between machine and gender is not rejected since the P-value is 0.946. The null hypothesis of no effect from machine is rejected since the P-value is 0.013. The null hypothesis of no effect from gender is not rejected since the P-value is 0.382.